Đề thi thử THPT QG năm 2022 môn Toán online – Đề thi của Trường THPT Thanh Đa giúp bạn ôn tập kiến thức một cách có hệ thống thông qua hệ thống câu hỏi đa dạng. Các câu hỏi được sắp xếp từ dễ đến khó giúp bạn tiếp cận kiến thức từng bước. Đặc biệt phù hợp với những bạn đang ôn thi. Thông qua quá trình làm bài, bạn có thể nhận ra lỗ hổng kiến thức. Điều này giúp việc học trở nên chủ động hơn.
Đề thi thử THPT QG năm 2022 môn Toán online – Đề thi của Trường THPT Thanh Đa
Câu 1: Cho hàm số $y = \dfrac{{2x + 1}}{{x + 2}}$. Khẳng định nào dưới đây đúng?
Câu 2: Với $a$ là số thực dương khác $1$ tùy ý, ${\log _{{a^2}}}{a^3}$ bằng
Câu 3: Hàm số $y = \dfrac{1}{3}{x^3} + {x^2} - 3x + 1$ đạt cực tiểu tại điểm
Câu 4: Thể tích của khối chóp có diện tích đáy bằng $6$ và chiều cao bằng $4$ là
Câu 5: Cho hình hộp đứng $ABCD.A'B'C'D'$ có đáy $ABCD$ là hình thoi có hai đường chéo $AC = a$, $BD = a\sqrt 3 $ và cạnh bên $AA' = a\sqrt 2 $. Thể tích $V$ của khối hộp đã cho là
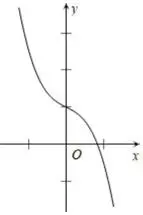
Câu 6: Cho hàm số $y = a{x^3} + b{x^2} + cx + d$ $\left( {a \ne 0} \right)$ có đồ thị như hình dưới đây. Khẳng định nào dưới đây đúng?
Câu 7: Cho hàm số $y = f\left( x \right)$ có bảng xét dấu của đạo hàm như sau. Hàm số $y = - 2f\left( x \right) + 2019$ nghịch biến trên khoảng nào trong các khoảng dưới đây?
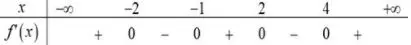
Câu 8: Cho $a$ và $b$ lần lượt là số hạng thứ hai và thứ mười của một cấp số cộng có công sai $d \ne 0.$ Giá trị của biểu thức ${\log _2}\left( {\dfrac{{b - a}}{d}} \right)$ là một số nguyên có số ước tự nhiên bằng
Câu 9: Cho khối chóp tứ giác $S.ABCD$có đáy $ABCD$ là hình thoi và $SABC$ là tứ diện đều cạnh $a$. Thể tích $V$ của khối chóp $S.ABCD$ là
Câu 10: Cho khối chóp tam giác $S.ABC$ có đỉnh $S$ và đáy là tam giác $ABC$. Gọi $V$ là thể tích của khối chóp. Mặt phẳng đi qua trọng tâm của ba mặt bên của khối chóp chia khối chóp thành hai phần. Tính theo $V$ thể tích của phần chứa đáy của khối chóp.
Câu 11: Cho mặt cầu $\left( S \right)$ tâm $O$, bán kính bằng 2. $\left( P \right)$ là mặt phẳng cách $O$ một khoảng bằng 1 và cắt $\left( S \right)$ theo một đường tròn $\left( C \right)$. Hình nón $\left( N \right)$ có đáy là $\left( C \right)$, đỉnh thuộc $\left( S \right)$, đỉnh cách $\left( P \right)$ một khoảng lớn hơn $2$. Kí hiệu ${V_1}$, ${V_2}$ lần lượt là thể tích của khối cầu $\left( S \right)$ và khối nón $\left( N \right)$. Tỉ số $\dfrac{{{V_1}}}{{{V_2}}}$ là
Câu 12: Tìm tất cả các giá trị thực của tham số $m$ để phương trình ${x^3} - 3mx + 2 = 0$ có nghiệm duy nhất.
Câu 13: Cho hình chóp $S.ABC$ có tam giác $ABC$ vuông tại $B$, $\widehat C = 60^\circ $, $AC = 2$, $SA \bot \left( {ABC} \right)$, $SA = 1$. Gọi $M$ là trung điểm của $AB$. Khoảng cách $d$ giữa $SM$ và $BC$ là
Câu 14: Gọi $M$ và $m$ lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số $y = \dfrac{{3\cos x - 1}}{{3 + \cos x}}$. Tổng $M + m$ là
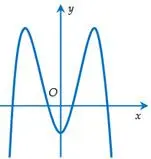
Câu 15: Cho hàm số $y = a{x^4} + b{x^2} + c$ ($a \ne 0$) có đồ thị như hình vẽ dưới đây. Mệnh đề nào dưới đây đúng?
Câu 16: Cho hình chóp $S.ABCD$ có đáy $ABCD$ là hình chữ nhật, $AB = AD\sqrt 2 $, $SA \bot \left( {ABC} \right)$. Gọi $M$ là trung điểm của $AB$. Góc giữa hai mặt phẳng $\left( {SAC} \right)$ và $\left( {SDM} \right)$ bằng
Câu 17: Trong mặt phẳng với hệ tọa độ $Oxy$, cho hai đường tròn $\left( {{C_1}} \right)$ và $\left( {{C_2}} \right)$ lần lượt có phương trình ${\left( {x - 1} \right)^2} + {\left( {y - 2} \right)^2} = 1$ và ${\left( {x + 1} \right)^2} + {y^2} = 1$. Biết đồ thị hàm số $y = \dfrac{{ax + b}}{{x + c}}$ đi qua tâm của $\left( {{C_1}} \right)$, đi qua tâm của $\left( {{C_2}} \right)$ và có các đường tiệm cận tiếp xúc với cả $\left( {{C_1}} \right)$ và $\left( {{C_2}} \right)$. Tổng $a + b + c$ là
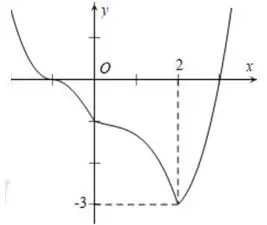
Câu 18: Cho hàm số $y = f\left( x \right)$ có đồ thị như hình dưới đây. Tìm tất cả các giá trị thực của tham số $m$ để bất phương trình $2f\left( x \right) + {x^2} > 4x + m$ nghiệm đúng với mọi $x \in \left( { - 1;3} \right)$.
Câu 19: Cho $x \in \left( {0;\dfrac{\pi }{2}} \right)$. Biết $\log \sin x + \log \cos x = - 1$ và $\log \left( {\sin x + \cos x} \right) = \dfrac{1}{2}\left( {\log n - 1} \right)$. Giá trị của $n$ là
Câu 20: Cho tứ diện $ABCD$. Trên các cạnh $AB$,$BC$, $CA$, $AD$ lần lượt lấy 3; 4; 5; 6 điểm phân biệt khác các điểm $A$, $B$, $C$, $D$. Số tam giác phân biệt có các đỉnh là các điểm vừa lấy là
Câu 21: Cho hình chóp đều $S.ABC$ có độ dài cạnh đáy bằng $2$, điểm $M$ thuộc cạnh $SA$ sao cho $SA = 4SM$ và $SA$ vuông góc với mặt phẳng $\left( {MBC} \right)$. Thể tích $V$ của khối chóp $S.ABC$ là
Câu 22: Cho hình trụ có hai đáy là hai hình tròn $\left( {O;R} \right)$ và $\left( {O';R} \right)$. $AB$ là một dây cung của đường tròn $\left( {O;R} \right)$ sao cho tam giác $O'AB$ là tam giác đều và mặt phẳng $\left( {O'AB} \right)$ tạo với mặt phẳng chứa đường tròn $\left( {O;R} \right)$ một góc $60^\circ $. Tính theo $R$ thể tích $V$ của khối trụ đã cho.
Câu 23: Biết ${\log _2}\left( {\sum\limits_{k = 1}^{100} {\left( {k \times {2^k}} \right)} - 2} \right) = a + {\log _c}b$ với $a$,$b$,$c$ là các số nguyên và $a > b > c > 1$. Tổng $a + b + c$ là
Câu 24: Số giá trị nguyên của tham số $m$ nằm trong khoảng $\left( {0;2020} \right)$ để phương trình $\left| {\left| {x - 1} \right| - \left| {2019 - x} \right|} \right| = 2020 - m$ có nghiệm là
Câu 25: Một cái hộp có dạng hình hộp chữ nhật có thể tích bằng $48$ và chiều dài gấp đôi chiều rộng. Chất liệu làm đáy và 4 mặt bên của hộp có giá thành gấp ba lần giá thành của chất liệu làm nắp hộp. Gọi $h$ là chiều cao của hộp để giá thành của hộp là thấp nhất. Biết $h = \dfrac{m}{n}$ với $m$, $n$ là các số nguyên dương nguyên tố cùng nhau. Tổng $m + n$ là
Câu 26: Cho hàm số $f\left( x \right) = m{x^4} + n{x^3} + p{x^2} + qx + r$ $\left( {m \ne 0} \right)$. Chia $f\left( x \right)$ cho $x - 2$ được phần dư bằng $2019$, chia $f'\left( x \right)$ cho $x - 2$ được phần dư bằng 2018. Gọi $g\left( x \right)$ là phần dư khi chia $f\left( x \right)$ cho ${\left( {x - 2} \right)^2}$. Giá trị của $g\left( { - 1} \right)$ là
Câu 27: Cho hình chóp tứ giác đều $S.ABCD$ có cạnh đáy bằng $a$, cạnh bên bằng $\sqrt 2 a$. Độ lớn của góc giữa đường thẳng $SA$ và mặt phẳng đáy bằng:
Câu 28: Hình vẽ là đồ thị của hàm số:
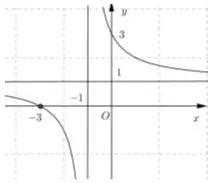
Câu 29: Đường thẳng $\left( \Delta \right)$ là giao của hai mặt phẳng $x + z - 5 = 0$ và $x - 2y - z + 3 = 0$ thì có phương trình là:
Câu 30: Mặt phẳng $\left( P \right)$ đi qua $A\left( {3;0;0} \right),\,\,B\left( {0;0;4} \right)$ và song song trục $Oy$ có phương trình:
Câu 31: Cho lăng trụ đều $ABC.A'B'C'$ có $AB = 2\sqrt 3 ,\,\,BB' = 2$.Gọi $M,\,\,N,\,\,P$ tương ứng là trung điểm của $A'B',\,\,A'C',\,\,BC$. Nếu gọi $\alpha $ là độ lớn của góc của hai mặt phẳng $\left( {MNP} \right)$ và $\left( {ACC'} \right)$ thì $\cos \alpha $ bằng:
Câu 32: Lăng trụ có chiều cao bằng $a$, đáy là tam giác vuông cân và có thể tích bằng $2{a^3}$. Cạnh góc vuông của đáy lăng trụ bằng
Câu 33: Tổng các nghiệm của phương trình ${4^x} - {6.2^x} + 2 = 0$ bằng:
Câu 34: Xét các số phức $z$ thỏa mãn $\left| {z - 1 - 3i} \right| = 2$. Số phức $z$ mà $\left| {z - 1} \right|$ nhỏ nhất là:
Câu 35: Cho hàm số $f\left( x \right) = \left\{ \begin{array}{l}{e^x} + m\,\,\,khi\,\,x \ge 0\\2x\sqrt {3 + {x^2}} \,\,khi\,\,x < 0\end{array} \right.$ liên tục trên và $\int\limits_{ - 1}^1 {f\left( x \right)dx} = ae + b\sqrt 3 + c$, $\left( {a,b,c \in \mathbb{Q}} \right)$. Tổng $T = a + b + 3c$ bằng:
Câu 36: Cho hình chóp đều $S.ABCD$ có cạnh đáy bằng $2$và cạnh bên bằng $2\sqrt 2 $. Gọi $\alpha $là góc của mặt phẳng $\left( {SAC} \right)$ và mặt phẳng $\left( {SAB} \right)$. Khi đó $\cos \alpha $ bằng:
Câu 37: Trong không gian $Oxyz$, cho $A\left( {2;0;0} \right),\,\,B\left( {0;4;0} \right),\,\,C\left( {0;0;6} \right),\,\,D\left( {2;4;6} \right)$. Gọi $\left( P \right)$ là mặt phẳng song song với $mp\left( {ABC} \right)$, $\left( P \right)$ cách đều $D$ và mặt phẳng $\left( {ABC} \right)$. Phương trình của $\left( P \right)$ là:
Câu 38: Số nào sau đây là điểm cực đại của hàm số $y = {x^4} - 2{x^3} + {x^2} + 2$?
Câu 39: Cho hàm số $f\left( x \right)$ có đạo hàm liên tục trên $\mathbb{R}$, $f\left( 0 \right) = 0,\,\,f'\left( 0 \right) \ne 0$ và thỏa mãn hệ thức$f\left( x \right)/f'\left( x \right) + 18{x^2} = \left( {3{x^2} + x} \right)f'\left( x \right) + \left( {6x + 1} \right)f\left( x \right)\,\,\forall x \in \mathbb{R}$. Biết $\int\limits_0^1 {\left( {x + 1} \right){e^{f\left( x \right)}}dx} = a{e^2} + b\,\,\left( {a,\,\,b \in \mathbb{Q}} \right)$. Giá trị của $a - b$ bằng:
Câu 40: Hàm số $y = - {x^3} + 3{x^2} - 2$ đồng biến trên khoảng:
Câu 41: Cho hàm số $f\left( x \right)$ liên tục trên $\mathbb{R}$ và $\int\limits_0^4 {f\left( x \right)dx} = 10,\,\,\int\limits_3^4 {f\left( x \right)dx} = 4$. Tích phân $\int\limits_0^3 {f\left( x \right)dx} $ bằng:
Câu 42: Một hộp có 10 quả cầu xanh, 5 quả cầu đỏ. Lấy ngẫu nhiên 5 quả từ hộp đó. Xác suất để được 5 quả có đủ hai màu là:
Câu 43: Tập xác định của hàm số $y = {\left[ {\ln \left( {x - 2} \right)} \right]^\pi }$ là:
Câu 44: Cho hình hộp chữ nhật $ABCD.A'B'C'D'$ có $AB = a,\,\,AD = AA' = 2a$. Khoảng cách giữa hai đường thẳng $AC$ và $DC'$ bằng:
Câu 45: Hàm số $y = f\left( x \right)$ có đạo hàm liên tục trên $\mathbb{R}$ và dấu của đạo hàm được cho bởi bảng dưới đây: Hàm số $y = f\left( {2x - 2} \right)$ nghịch biến trên khoảng:

Câu 46: Cho $n \in {\mathbb{N}^*}$ và $C_n^2.C_n^{n - 2} + C_n^8.C_n^{n - 8} = 2C_n^2.C_n^{n - 8}$ . Tổng $T = {1^2}C_n^1 + {2^2}C_n^2 + ... + {n^2}C_n^n$ bằng:
Câu 47: Cho $n \in \mathbb{N}$ và $n! = 1$. Số giá trị của $n$ thỏa mãn giả thiết đã cho là:
Câu 48: Cho hàm số có đồ thị như hình dưới đây. Hàm số $g\left( x \right) = \ln \left( {f\left( x \right)} \right)$ đồng biến trên khoảng nào dưới đây?
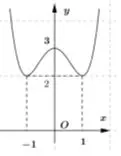
Câu 49: Cần sản xuất một vỏ hộp sữa hình trụ có thể tích $V$ cho trước. Để tiết kiệm vật liệu nhất thì bán kính đáy phải bằng
Câu 50: Bất phương trình ${4^x} - \left( {m + 1} \right){2^{x + 1}} + m \ge 0$ nghiệm đúng với mọi $x \ge 0$. Tập tất cả các giá trị của $m$ là: