Thi thử tốt nghiệp THPT quốc gia môn Toán online – Đề thi của trường THPT Hà Huy Tập năm 2022 giúp bạn đánh giá chính xác mức độ hiểu bài thông qua nội dung bám sát chương trình học. Các câu hỏi được thiết kế khoa học giúp bạn học mà không cảm thấy áp lực. Đặc biệt phù hợp với học sinh muốn cải thiện điểm số. Thông qua quá trình làm bài, bạn có thể xác định phần kiến thức còn yếu. Điều này giúp việc học trở nên có mục tiêu rõ ràng hơn.
Thi thử tốt nghiệp THPT quốc gia môn Toán online – Đề thi của trường THPT Hà Huy Tập năm 2022
Câu 1: Khẳng định nào dưới đây về tính đơn điệu của hàm số $y = {x^3} + 3{x^2} - 9x - 2019$ là đúng ?
Câu 2: Cho $\dfrac{{{5^2}\sqrt[3]{5}}}{{{5^{\frac{1}{2}}}}} = {5^x}$ . Giá trị của $x$ là
Câu 3: Cho hình bình hành $MNPQ$. Phép tịnh tiến theo véc tơ $\overrightarrow {MN} $ biến điểm $Q$ thành điểm nào sau đây?
Câu 4: Cho hình chóp $S.ABC$ có đáy $ABC$ là tam giác vuông cân tại $B;BA = a;SA = a\sqrt 2 $ và $SA$ vuông góc với mặt phẳng đáy. Góc giữa $SC$ và mặt phẳng $\left( {SAB} \right)$ bằng bao nhiêu?
Câu 5: Cho số thực dương $x$, biểu thức rút gọn của $P = \dfrac{{\sqrt[3]{x}.{x^{ - 2}}.{x^3}}}{{\sqrt x .\sqrt[6]{x}}}$ là:
Câu 6: Cắt khối trụ có bán kính đáy bằng $5$ và chiều cao bằng $10$ bởi một mặt phẳng song song với trục và cách trục một khoảng bằng $3$ ta được thiết diện là
Câu 7: Khối lăng trụ tam giác đều có cạnh đáy bằng $2\sqrt 3 a$, cạnh bên bằng $3\sqrt 3 a$ có thể tích bằng
Câu 8: Cho $a > 0$ và $a \ne 1.$ Giá trị của biểu thức ${a^{{{\log }_{\sqrt a }}3}}$ bằng
Câu 9: Cho dãy số $\left( {{u_n}} \right)$ xác định bởi $\left\{ \begin{array}{l}{u_1} = 3\\{u_{n + 1}} = 2{u_n} - 5,\forall n \ge 1\end{array} \right.$. Số hạng thứ $3$ của dãy số đã cho là
Câu 10: Tiếp tuyến với đồ thị hàm số $y = {x^4} - 3{x^2} + 2018$ tại điểm có hoành độ bằng $1$ có phương trình
Câu 11: Khối chóp có diện tích đáy bằng $6$ và chiều cao bằng $2$ thì có thể tích bằng
Câu 12: Đường cong trong hình vẽ bên là đồ thị của hàm số nào?
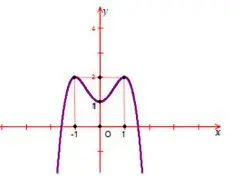
Câu 13: Khối lăng trụ tam giác có bao nhiêu mặt?
Câu 14: Hàm số $y = {x^4} - 2{x^2} + 3$ có số điểm cực trị là
Câu 15: Phương trình $2\sin x = 1$ có một nghiệm là
Câu 16: Tìm $I = \lim \dfrac{{3n - 2}}{{n + 1}}$
Câu 17: Phương trình đường tiệm cận đứng của đồ thị hàm số $y = \dfrac{{2 - 2x}}{{x + 1}}$ là
Câu 18: Giá trị cực tiểu của hàm số $y = {x^2} - 4x + 3$ là
Câu 19: Tập xác định của hàm số $y = {\pi ^{ - x}}$ là
Câu 20: Có bao nhiêu số tự nhiên có $5$ chữ số khác nhau?
Câu 21: Cho hai mặt phẳng song song $\left( P \right),\left( Q \right)$ và đường thẳng $\Delta $. Mệnh đề nào sau đây sai?
Câu 22: Tính đạo hàm của hàm số $y = \ln \left( {{x^2} + x + 1} \right)$.
Câu 23: Hình nón bán kính đáy $R$ và đường sinh $l$ thì có diện tích xung quanh bằng
Câu 24: Cắt khối cầu tâm $I$, bán kính $R = 5$ bởi một mặt phẳng $\left( P \right)$ cách $I$ một khoảng bằng $4$, diện tích thiết diện là
Câu 25: Một người mau một căn hộ trị giá $800$ triệu theo hình thức trả góp với lãi suất $0,8\% $/tháng. Lúc đầu người đó trả $200$ triệu, số tiền còn lại mỗi tháng người đó trả cả gốc lẫn lãi $20$ triệu. Hỏi sau ít nhất bao nhiêu tháng người đó trả hết nợ, biết rằng lãi suất chỉ tính trên số tiền còn nợ? (Kết quả làm tròn đến hàng đơn vị)
Câu 26: Giá trị lớn nhất của hàm số $y = x{e^{ - x}}$ trên đoạn $\left[ {0;2} \right]$ bằng
Câu 27: Cho tứ diện đều $ABCD$ có cạnh bằng $4$. Gọi $M,N,P,Q,R,S$ theo thứ tự là trung điểm các cạnh $AB,AC,CD,BD,AD,BC$. Thể tích khối bát diện đều $RMNPQS$ là
Câu 28: Cho hai số thực $x;y$ thỏa mãn $0 < x < 1 {\log _{\frac{1}{y}}}x$ $\left( 2 \right)\,{\log _y}\left( {1 + x} \right) > {\log _x}y$ $\left( 3 \right)\,{\log _y}x < {\log _{1 + x}}\left( {1 + y} \right)$
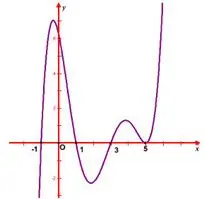
Câu 29: Cho hàm số $y = f\left( x \right)$ có đạo hàm trên $\mathbb{R}$ và $y = f'\left( x \right)$ có đồ thị như hình vẽ. Phương trình $f\left( x \right) = m$ ($m$ là tham số) có nhiều nhất bao nhiêu nghiệm trong khoảng $\left( { - 2;6} \right)$?
Câu 30: Tìm tất cả các giá trị của tham số $m$ để đồ thị hàm số $y = {x^4} - 2{m^2}{x^2} + 2m$ có ba điểm cực trị $A,B,C$ sao cho $O,A,B,C$ là các đỉnh của một hình thoi (với $O$ là gốc tọa độ).
Câu 31: Trong khai triển ${\left( {1 + x + {x^2}} \right)^n} = {a_0} + {a_1}x + ... + {a_{2n}}{x^{2n}}$ có $\dfrac{{{a_1}}}{2} = \dfrac{{{a_2}}}{{11}}$ thì giá trị của $n$ là
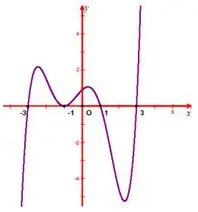
Câu 32: Cho hàm số $f\left( x \right) = \left( {x + 3} \right){\left( {x + 1} \right)^2}\left( {x - 1} \right)\left( {x - 3} \right)$ có đồ thị như hình vẽ. Đồ thị hàm số $g\left( x \right) = \dfrac{{\sqrt x }}{{f\left( x \right) + 3}}$ có bao nhiêu đường tiệm cận?
Câu 33: Có bao nhiêu giá trị nguyên trong tập giá trị của hàm số $y = \dfrac{{{{\sin }^2}x - 2\sin 2x + 1}}{{\cos 2x + 2\sin 2x - 3}}$?
Câu 34: Cho hàm số $y = {x^3} + 1$ có đồ thị $\left( C \right)$. Tìm điểm có hoành độ dương trên đường thẳng $d:y = x + 1$ mà qua đó kẻ được đúng hai tiếp tuyến tới $\left( C \right).$
Câu 35: Cho hình chóp $S.ABCD$ có đáy $ABCD$ là hình thang vuông tại$A$ và $D$, $AD = DC = a$. Biết $SAB$ là tam giác đều cạnh $2a$ và mặt phẳng $\left( {SAB} \right)$ vuông góc với mặt phẳng $\left( {ABCD} \right)$. Tính cô sin của góc giữa hai mặt phẳng $\left( {SAB} \right)$ và $\left( {SBC} \right)$.
Câu 36: Cho hình trụ $\left( T \right)$ có chiều cao bằng đường kính đáy, hay đáy là các hình tròn $\left( {O;R} \right)$ và $\left( {O';R} \right)$. Gọi $A$ là điểm di động trên đường tròn $\left( {O;R} \right)$ và $B$ là điểm di động trên đường tròn $\left( {O';R} \right)$, khi đó thể tích khối tứ diện $OO'AB$ có giá trị lớn nhất là
Câu 37: Nhà cung cấp dịch vị internet X áp dụng mức giá với dung lượng sử dụng của khách hàng theo hình thức bậc thang như sau: Mỗi bậc áp dụng cho $64MB$, bậc 1 có giá $100$ đ/1MB, giá của mỗi MB ở các bậc tiếp theo giảm $10\% $ so với bậc trước đó. Tháng 12 năm 2018, bạn An sử dụng hết $2GB$, hỏi bạn An phải trả bao nhiêu tiền (tính bằng đồng, làm tròn đến hàng đơn vị)?
Câu 38: Một công ty cần sản xuất các sản phẩm bằng kim loại có dạng khối lăng trụ tam giác đều có thể tích bằng $\sqrt[4]{3}\left( {{m^3}} \right)$ rồi sơn lại hai mặt đáy và hai mặt bên. Hỏi diện tích cần sơn mỗi sản phẩm nhỏ nhất bằng bao nhiêu mét vuông?
Câu 39: Một quân Vua ở giữa một bàn cờ vua (như hình vẽ) di chuyển ngẫu nhiên $3$ bước, tìm xác suất để sau $3$ bước nó trở lại vị trí xuất phát (mỗi bước đi, quân Vua chỉ có thể đi sang ô chung đỉnh hoặc ô chung cạnh với ô nó đang đứng).
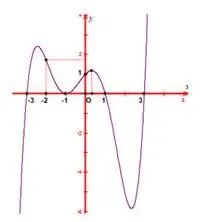
Câu 40: Cho hàm số $y = f\left( x \right)$ liên tục trên $\mathbb{R}$ và có đồ thị như hình vẽ. Có bao nhiêu giá trị nguyên của $m$ để phương trình $\left| {f\left( {\left| {x - 2} \right|} \right) + 1} \right| - m = 0$ có $8$ nghiệm phân biệt trong khoảng $\left( { - 5;5} \right)?$
Câu 41: Cho hình chóp tứ giác đều $S.ABCD$ có cạnh đáy bằng $a$, cạnh bên bằng $2a$. Mặt phẳng $\left( \alpha \right)$ qua $A$ và song song với $BD$ cắt cạnh $SC$ tại $I$ và chia khối chóp thành $2$ phần có thể tích bằng nhau. Tính diện tích thiết diện của hình chóp $S.ABCD$ khi cắt bởi mặt phẳng $\left( \alpha \right)$.
Câu 42: Cho hình chóp $S.ABCD$ có đáy $ABCD$ là hình thang cân $\left( {AB//CD} \right)$. Biết $AD = 2\sqrt 5 ;AC = 4\sqrt 5 ;AC \bot AD;SA = SB = SC = SD = 7.$ Tính khoảng cách giữa hai đường thẳng $SA,CD.$
Câu 43: Tìm tất cả các giá trị của tham số $m$ để hàm số $y = \dfrac{x}{2} - \sqrt {{x^2} - x + m} $ đồng biến trên $\left( { - \infty ;2} \right)$.
Câu 44: Gọi $M;m$ lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số $y = \dfrac{{x + a}}{{{x^2} + 1 + 2a}}$, với $a$ là tham số dương. Tìm tất cả các giá trị của $a$ để $3M + 7m = 0.$
Câu 45: Cho ${\log _2}3 = a,{\log _3}5 = b$, giá trị của biểu thức $P = {\log _{20}}36 - {\log _{75}}12$ tính theo $a,b$ là
Câu 46: Cho tứ diện $ABCD$, có $AB = CD = 5$, khoảng cách giữa $AB$ và $CD$ bằng $12$, góc giữa hai đường thẳng $AB$ và $CD$ bằng ${30^0}$. Tính thể tích khối tứ diện $ABCD$ .
Câu 47: Phương trình ${\sin ^2}x + \sin x\sin 2x = m\cos x + 2m{\cos ^2}x$ (với $m$ là tham số) có ít nhất bao nhiêu nghiệm trong khoảng $\left( { - \pi ;\dfrac{{3\pi }}{2}} \right)$?
Câu 48: Tìm tất cả các giá trị của $m$ để hàm số $y = \cos 2x + mx$ đồng biến trên $\mathbb{R}.$
Câu 49: Cho $a;b$ là các số thực thỏa mãn $a > 0$ và $a \ne 1$ biết phương trình ${a^x} - \frac{1}{{{a^x}}} = 2\cos \left( {bx} \right)$ có 7 nghiệm thực phân biệt. Tìm số nghiệm thực phân biệt của phương trình ${a^{2x}} - 2{a^x}\left( {{\mathop{\rm cosbx}\nolimits} + 2} \right) + 1 = 0$
Câu 50: Tìm hàm số đồng biến trên $\mathbb{R}$ .