Thi thử tốt nghiệp THPT quốc gia môn Toán online – Đề thi của trường THPT Trần Khai Nguyên năm 2022

Câu 1: Tìm tất cả các giá trị của tham số m để phương trình ${x^3} + 3{x^2} - 2 = m$ có hai nghiệm phân biệt.

• A. $m \in \left( { - \infty ; - 2} \right]$
• B. $m \notin \left[ { - 2;\;2} \right]$
• C. $m \in \left[ {2; + \infty } \right)$
• D. $m \in \left\{ { - 2;\;2} \right\}$

Câu 2: Trên đồ thị $\left( C \right):\,\,y = \dfrac{{x + 1}}{{x + 2}}$ có bao nhiêu điểm M mà tiếp tuyến với $\left( C \right)$ tại M song song với đường thẳng $d:\,\,x + y = 1$.

• A. 0
• B. 4
• C. 3
• D. 2

Câu 3: Xác định các hệ số $a,\;b,\;c$ để đồ thị hàm số $y = \dfrac{{ax - 1}}{{bx + c}}$ có đồ thị hàm số như hình vẽ bên:

• A. $a = 2,\;b = 2,\;c = - 1$
• B. $a = 2,\;b = - 1,\;c = 1$
• C. $a = 2,\;b = 1,\;c = 1$
• D. $a = 2,\;b = 1,\;c = - 1$

Câu 4: Cho hàm số $y = f\left( x \right)$ có $f'\left( x \right) > 0\,\,\forall x \in R$. Tìm tập hợp tất cả các giá trị thực của x để $f\left( {\dfrac{1}{x}} \right) < f\left( 1 \right)$.

• A. $\left( { - \infty ;0} \right) \cup \left( {0;1} \right)$
• B. $\left( { - \infty ;0} \right) \cup \left( {1; + \infty } \right)$
• C. $\left( { - \infty ;1} \right)$
• D. $\left( {0;1} \right)$

Câu 5: Cho hàm số $y = f\left( x \right)$ có đạo hàm $y' = {x^2}\left( {x - 2} \right).$ Mệnh đề nào sau đây đúng?

• A. Hàm số nghịch biến trên $R.$
• B. Hàm số đồng biến trên $\left( {0;\;2} \right).$
• C. Hàm số nghịch biến trên $\left( { - \infty ;\;0} \right)$ và $\left( {2; + \infty } \right)$
• D. Hàm số đồng biến trên $\left( {2; + \infty } \right).$

Câu 6: Cho cấp số nhân $\left( {{u_n}} \right)$ có ${u_1} = 2$ và biểu thức $20{u_1} - 10{u_2} + {u_3}$ đạt giá trị nhỏ nhất. Tìm số hạng thứ bảy của cấp số nhân $\left( {{u_n}} \right)$ ?

• A. 2000000
• B. 136250
• C. 39062
• D. 31250

Câu 7: Trong không gian $Oxyz,$ phương trình của mặt phẳng $\left( P \right)$ đi qua điểm $B\left( {2;\;1; - 3} \right)$ đồng thời vuông góc với hai mặt phẳng $\left( Q \right):\;x + y + 3z = 0,\;\;\left( R \right):\;\;2x - y + z = 0$ là:

• A. $4x + 5y - 3z + 22 = 0$
• B. $4x - 5y - 3z - 12 = 0$
• C. $2x + y - 3z - 14 = 0$
• D. $4x + 5y - 3z - 22 = 0$

Câu 8: Đặt $a = {\log _2}5$ và $b = {\log _3}5.$ Biểu diễn đúng của ${\log _6}5$ theo $a,\;b$ là:

• A. $\dfrac{1}{{a + b}}$
• B. $a + b$
• C. $\dfrac{{ab}}{{a + b}}$
• D. $\dfrac{{a + b}}{{ab}}$

Câu 9: Cho hai góc nhọn a và b thỏa mãn $\tan a = \dfrac{1}{7}$ và $\tan b = \dfrac{3}{4}$. Tính $a + b$.

• A. $\dfrac{\pi }{3}$
• B. $\dfrac{{2\pi }}{3}$
• C. $\dfrac{\pi }{6}$
• D. $\dfrac{\pi }{4}$

Câu 10: Một hình lăng trụ tam giác đều có nhiêu mặt phẳng đối xứng?

• A. 5
• B. 3
• C. 4
• D. 6

Câu 11: Công thức nào sau đây là sai?

• A. $\int\limits_{}^{} {{x^3}dx} = \dfrac{1}{4}{x^4} + C$
• B. $\int\limits_{}^{} {\dfrac{{dx}}{{{{\sin }^2}x}}} = \cot x + C$
• C. $\int\limits_{}^{} {\sin xdx} = - \cos x + C$
• D. $\int\limits_{}^{} {\dfrac{1}{x}dx} = \ln \left| x \right| + C$

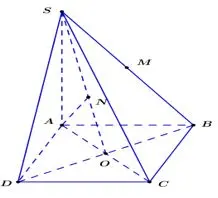
Câu 12: Cho hình chóp SABCD, có đáy ABCD là hình vuông tâm O, cạnh bên vuông góc với mặt đáy. Gọi M là trung điểm của SA, N là hình chiếu vuông góc của A lên SO. Mệnh đề nào sau đây đúng?

• A. $AC \bot \left( {SBD} \right)$
• B. $DN \bot \left( {SAB} \right)$
• C. $AN \bot \left( {SOD} \right)$
• D. $AM \bot \left( {SBC} \right)$

Câu 13: Gọi A, B lần lượt là các giá trị nhỏ nhất, giá trị lớn nhất của hàm số $y = \dfrac{{x + {m^2} + 2m}}{{x - 2}}$ trên đoạn $\left[ {3;4} \right]$. Tìm tất cả các giá trị thực của tham số m để $A + B = \dfrac{{19}}{2}$.

• A. $m = 1;m = - 3$
• B. $m = - 1;m = 3$
• C. $m = \pm 3$
• D. $m = - 4$

Câu 14: Trong mặt phẳng với hệ tọa độ Oxy cho hai điểm $A\left( { - 2;4} \right)$ và $B\left( {8;4} \right)$. Tìm tọa độ điểm C trên trục Ox, có hoành độ dương sao cho tam giác ABC vuông tại C.

• A. $C\left( {3;0} \right)$
• B. $C\left( {1;0} \right)$
• C. $C\left( {5;0} \right)$
• D. $C\left( {6;0} \right)$

Câu 15: Giá trị lớn nhất của hàm số $y = {x^2} + \dfrac{{16}}{x}$ trên đoạn $\left[ {\dfrac{3}{2};\;4} \right]$ bằng:

• A. $24$
• B. $20$
• C. $12$
• D. $\dfrac{{155}}{{12}}$

Câu 16: Cắt khối trụ bởi một mặt phẳng qua trục ta được thiết diện là hình chữ nhật ABCD có AB và CD thuộc hai đáy hình trụ, $AB = 4a;\,\,AC = 5a$. Tính thể tích khối trụ:

• A. $V = 8\pi {a^3}$
• B. $V = 16\pi {a^3}$
• C. $V = 12\pi {a^3}$
• D. $V = 4\pi {a^3}$

Câu 17: Cho hàm số $y = {\log _{\frac{1}{2}}}\left| x \right|.$ Mệnh đề nào dưới đây là mệnh đề sai?

• A. Hàm số đã cho nghịch biến trên từng khoảng xác định.
• B. Đồ thị hàm số đã cho không có tiệm cận ngang.
• C. Đồ thị hàm số đã cho có một tiệm cận đứng là trục tung.
• D. Hàm số đã cho có tập xác định là $D = R{\rm{\backslash }}\left\{ 0 \right\}.$

Câu 18: Cho x là số thực dương, khai triển nhị thức ${\left( {{x^2} + \dfrac{1}{x}} \right)^{12}}$ ta có hệ số của số hạng chứa ${x^m}$ bằng 792. Giá trị của m là:

• A. $m = 3$ và$m = 9$
• B. $m = 0$ và $m = 9$
• C. $m = 9$
• D. $m = 0$

Câu 19: Tìm tập nghiệm $S$ của phương trình ${2^{x + 1}} = 4.$

• A. $S = \left\{ 4 \right\}$
• B. $S = \left\{ 1 \right\}$
• C. $S = \left\{ 3 \right\}$
• D. $S = \left\{ 2 \right\}$

Câu 20: Cho tứ diện ABCD có $\left( {ACD} \right) \bot \left( {BCD} \right),\,\,AC = AD = BC = BD = a,\,\,CD = 2x$. Giá trị của x để hai mặt phẳng (ABC) và (ABD) vuông góc với nhau là:

• A. $\dfrac{{a\sqrt 2 }}{3}$
• B. $\dfrac{{a\sqrt 3 }}{3}$
• C. $\dfrac{{a\sqrt 3 }}{2}$
• D. $\dfrac{{a\sqrt 5 }}{3}$

Câu 21: Cho khối chóp $SABCD$ có đáy là hình vuông cạnh $\dfrac{a}{{\sqrt 2 }},\;\;\Delta SAC$ vuông tại $S$ và nằm trong mặt phẳng vuông góc với đáy, cạnh bên $SA$ tạo với đáy góc ${60^0}.$ Tính thể tích $V$của khối chóp $SABCD.$

• A. $V = \dfrac{{{a^3}\sqrt 3 }}{{24}}$
• B. $V = \dfrac{{{a^3}\sqrt 3 }}{{12}}$
• C. $V = \dfrac{{{a^3}\sqrt 6 }}{{24}}$
• D. $V = \dfrac{{{a^3}\sqrt 2 }}{{24}}$

Câu 22: Nguyên hàm của hàm số $f\left( x \right) = 4{x^3} + x - 1$ là:

• A. ${x^4} + {x^2} + x + C$
• B. $12{x^2} + 1 + C$
• C. ${x^4} + \dfrac{1}{2}{x^2} - x + C$
• D. ${x^4} - \dfrac{1}{2}{x^2} - x + C$

Câu 23: Cho hàm số $y = f\left( x \right)$ có đạo hàm cấp 2 trên khoảng $K$ và ${x_0} \in K.$ Mệnh đề nào sau đây đúng?

• A. Nếu $f''\left( {{x_0}} \right) = 0$ thì ${x_0}$ là điểm cực trị của hàm số $y = f\left( x \right).$
• B. Nếu ${x_0}$ là điểm cực trị của hàm số $y = f\left( x \right)$ thì $f''\left( {{x_0}} \right) \ne 0.$
• C. Nếu ${x_0}$ là điểm cực trị của hàm số $y = f\left( x \right)$ thì $f'\left( {{x_0}} \right) = 0.$
• D. Nếu ${x_0}$ là điểm cực tiểu của hàm số $y = f\left( x \right)$ thì $f''\left( {{x_0}} \right) > 0.$

Câu 24: Tìm nguyên hàm của hàm số $f\left( x \right) = \dfrac{1}{{x{{\left( {\ln x + 2} \right)}^2}}}$.

• A. $\int\limits_{}^{} {f\left( x \right)dx} = \dfrac{1}{{\ln x + 2}} + C$
• B. $\int\limits_{}^{} {f\left( x \right)dx} = \dfrac{{ - 1}}{{\ln x + 2}} + C$
• C. $\int\limits_{}^{} {f\left( x \right)dx} = \dfrac{x}{{\ln x + 2}} + C$
• D. $\int\limits_{}^{} {f\left( x \right)dx} = \ln x + 2 + C$

Câu 25: Tính tích tất cả các nghiệm của phương trình ${2^{2{x^2} + 5x + 4}} = 4.$

• A. $1$
• B. $\dfrac{5}{2}$
• C. $ - \dfrac{5}{2}$
• D. $ - 1$

Câu 26: Cho hai góc lượng giác a và b. Trong các khẳng định sau, khẳng định nào là khẳng định sai?

• A. $\sin \left( {a + b} \right) = \sin a\cos b + \cos a\sin b$
• B. $\sin \left( {a - b} \right) = \sin a\cos b + \cos a\sin b$
• C. $\cos \left( {a + b} \right) = \cos a\cos b - \sin a\sin b$
• D. $\cos \left( {a - b} \right) = \cos a\cos b + \sin a\sin b$

Câu 27: Trong không gian với hệ trục tọa độ $Oxyz$ cho $\overrightarrow a = \left( {1; - 2;3} \right)$ và $\overrightarrow b = \left( {2; - 1; - 1} \right).$ Khẳng định nào sau đây đúng?

• A. Vecto $\overrightarrow a $ vuông góc với $\overrightarrow b $
• B. Vecto $\overrightarrow a $ cùng phương với $\overrightarrow b $
• C. $\left| {\overrightarrow a } \right| = \sqrt {14} $
• D. $\left[ {\overrightarrow a ,\;\overrightarrow b } \right] = \left( { - 5; - 7; - 3} \right)$

Câu 28: Cho hình chóp S.ABCD có $SC = x\,\,\left( {0 < x < a\sqrt 3 } \right)$, các cạnh còn lại đều bằng a. Biết rằng thể tích khối chóp S.ABCD lớn nhất khi và chỉ khi $x = \dfrac{{a\sqrt m }}{n}\,\,\left( {m,n \in {N^*}} \right)$. Mệnh đề nào sau đây đúng?

• A. $m + 2n = 10$
• B. $2{m^2} - 3n < 15$
• C. ${m^2} - n = 30$
• D. $4m - {n^2} = - 20$

Câu 29: Có bao nhiêu giá trị nguyên của tham số m để hàm số: $y = {x^8} + \left( {m + 1} \right){x^5} - \left( {{m^2} - 1} \right){x^4} + 1$ đạt cực tiểu tại $x = 0?$

• A. vô số
• B. 3
• C. 2
• D. 4

Câu 30: Có bao nhiêu giá trị nguyên của tham số m thuộc đoạn $\left[ { - 2018;2018} \right]$ để phương trình ${\left( {x + 2 - \sqrt {{x^2} + 1} } \right)^2} + \dfrac{{18\left( {{x^2} + 1} \right)\sqrt {{x^2} + 1} }}{{x + 2 + \sqrt {{x^2} + 1} }} = m\left( {{x^2} + 1} \right)$ có nghiệm thực?

• A. 25
• B. 2019
• C. 2018
• D. 2012

Câu 31: Tìm tất cả các giá trị của tham số $m$ để phương trình ${\left( {7 - 3\sqrt 5 } \right)^{{x^2}}} + m{\left( {7 + 3\sqrt 5 } \right)^{{x^2}}} = {2^{{x^2} - 1}}$ có đúng bốn nghiệm phân biệt.

• A. $0 < m < \dfrac{1}{{16}}$
• B. $0 \le m < \dfrac{1}{{16}}$
• C. $ - \dfrac{1}{2} < m < 0$
• D. $ - \dfrac{1}{2} < m \le \dfrac{1}{{16}}$

Câu 32: Trong không gian với hệ tọa độ Oxyz, cho $A\left( { - 3;0;0} \right);\,\,B\left( {0;0;3} \right);\,\,C\left( {0; - 3;0} \right)$ và mặt phẳng $\left( P \right):\,\,x + y + z - 3 = 0$. Tìm trên (P) điểm M sao cho $\left| {\overrightarrow {MA} + \overrightarrow {MB} - \overrightarrow {MC} } \right|$ nhỏ nhất.

• A. $M\left( {3;3; - 3} \right)$
• B. $M\left( {3; - 3;3} \right)$
• C. $M\left( { - 3;3;3} \right)$
• D. $M\left( { - 3; - 3;3} \right)$

Câu 33: Có bao nhiêu giá trị nguyên của tham số m để bất phương trình $\log \left( {2{x^2} + 3} \right) < \log \left( {{x^2} + mx + 1} \right)$ có tập nghiệm là $R.$

• A. vô số
• B. 2
• C. 5
• D. 0

Câu 34: Gọi M là giá trị lớn nhất của hàm số $f\left( x \right) = 6\sqrt {{x^2} - 6x + 12} + 6x - {x^2} - 4$. Tính tích các nghiệm của phương trình $f\left( x \right) = M$.

• A. -6
• B. 3
• C. -3
• D. 6

Câu 35: Gọi $F\left( x \right)$ là một nguyên hàm của hàm số $f\left( x \right) = {x^3} - 2{x^2} + 1$ thỏa mãn $F\left( 0 \right) = 5.$ Khi đó phương trình $F\left( x \right) = 5$ có số nghiệm thực là:

• A. 0
• B. 1
• C. 2
• D. 3

Câu 36: Cho hàm số $y = f\left( x \right)$ có đạo hàm $y' = {x^2} - 3x + {m^2} + 5m + 6.$ Tìm tất cả các giá trị của m để hàm số đồng biến trên $\left( {3;\;5} \right).$

• A. $m \in \left( { - \infty ; - 3} \right) \cup \left( { - 2; + \infty } \right)$
• B. $m \in \left( { - \infty ; - 3} \right] \cup \left[ { - 2; + \infty } \right)$
• C. $m \in \left[ { - 3;\; - 2} \right]$
• D. Với mọi $m \in R.$

Câu 37: Một giải thi đấu bóng đá quốc gia có 12 đội bóng thi đấu vòng tròn hai lượt tính điểm (2 đội bất kì thi đấu với nhau đúng 2 trận). Sau mỗi trận đấu, đội thắng 3 điểm, đội thua 0 điểm, nếu hòa mỗi đội được 1 điểm. Sau giải đấu ban tổ chức ban tổ chức thống kê được 60 trận hòa. Hỏi tổng số điểm của tất cả các đội sau giải đấu là:

• A. 336
• B. 630
• C. 360
• D. 306

Câu 38: Một hộp sữa hình trụ có thể tích V (không đổi) được làm từ một tấm tôn có diện tích đủ lớn. Nếu hộp sữa chỉ kín một đáy thì để tốn ít vật liệu nhất, hệ thức giữa bán kính đáy R và đường cao h bằng:

• A. $h = \sqrt 3 R$
• B. $h = \sqrt 2 R$
• C. $h = 2R$
• D. $h = R$

Câu 39: Tập hợp tất cả các giá trị của tham số m để hàm số $y = \dfrac{{4x + 7}}{{{{\log }_{2018}}\left( {{x^2} - 2x + {m^2} - 6m + 10} \right)}}$ xác định với mọi $x \in R$ là:

• A. $\left( {2;4} \right)\backslash \left\{ 3 \right\}$
• B. $\left[ {2;4} \right]\backslash \left\{ 3 \right\}$
• C. $\left[ {4; + \infty } \right)$
• D. $\left( { - \infty ;2} \right) \cup \left( {4; + \infty } \right)$

Câu 40: Cho tứ diện $ABCD$ có $AD \bot \left( {ABC} \right),\;ABC$ có tam giác vuông tại $B.$ Biết $BC = 2a,\;\;AB = 2a\sqrt 3 ,\;\;AD = 6a.$ Quay tam giác $ABC$ và $ABD$ (bao gồm cả điểm bên trong 2 tam giác) xung quanh đường thẳng $AB$ ta được hai khối tròn xoay. Thể tích phần chung của 2 khối tròn xoay đó bằng:

• A. $\dfrac{{5\sqrt 3 \pi {a^3}}}{2}$
• B. $\dfrac{{3\sqrt 3 \pi {a^3}}}{2}$
• C. $\dfrac{{64\sqrt 3 \pi {a^3}}}{3}$
• D. $\dfrac{{4\sqrt 3 \pi {a^3}}}{2}$

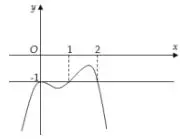
Câu 41: Cho hàm số $y = f\left( x \right)$ xác định và liên tục trên R, có đạo hàm $f'\left( x \right)$. Biết rằng đồ thị hàm số $f'\left( x \right)$ như hình vẽ. Xác định điểm cực đại của hàm số $g\left( x \right) = f\left( x \right) + x$.

• A. Không có cực trị
• B. $x = 0$
• C. $x = 1$
• D. $x = 2$

Câu 42: Cho hàm số $f\left( x \right)$ thỏa mãn ${\left[ {f'\left( x \right)} \right]^2} + f\left( x \right).f''\left( x \right) = {x^3} - 2x\;\;\forall x \in R$ và $f\left( 0 \right) = f'\left( 0 \right) = 2.$ Tính giá trị của $T = {f^2}\left( 2 \right).$

• A. $\dfrac{{268}}{{15}}$
• B. $\dfrac{{160}}{{15}}$
• C. $\dfrac{{268}}{{30}}$
• D. $\dfrac{4}{{15}}$

Câu 43: Cho hình chóp S.ABCD có đáy ABCD là hình thang vuông tại A, D, cạnh bên SA vuông góc với mặt đáy. Biết $AB = 2AD = 2DC = 2a$, góc giữa hai mặt phẳng (SAB) và (SBC) là ${60^0}$. Độ dài cạnh SA là:

• A. $a\sqrt 2 $
• B. $2a\sqrt 3 $
• C. $3a\sqrt 2 $
• D. $a\sqrt 3 $

Câu 44: Cho hàm số $y = \dfrac{{3x + b}}{{ax - 2}}\;\;\left( {ab \ne - 2} \right).$ Biết rằng $a$ và $b$ là các giá trị thỏa mãn tiếp tuyến của đồ thị hàm số tại điểm $A\left( {1; - 4} \right)$ song song với đường thẳng $d:\;7x + y - 4 = 0.$ Khi đó giá trị của $a - 3b$ bằng:

• A. -2
• B. 4
• C. 5
• D. -1

Câu 45: Trong không gian với hệ trục tọa độ Oxyz cho ba mặt phẳng $\left( P \right):\,\,x - 2y + z - 1 = 0$; $\left( Q \right):\,\,x - 2y + z + 8 = 0;\,\,\left( R \right):\,\,x - 2y + z - 4 = 0$. Một đường thẳng d thay đổi cắt ba mặt $\left( P \right),\,\,\left( Q \right),\,\,\left( R \right)$ lần lượt tại A, B, C. Tìm giá trị nhỏ nhất của $T = A{B^2} + \dfrac{{144}}{{A{C^2}}}$.

• A. 24
• B. 36
• C. 72
• D. 144

Câu 46: Cho khối nón có bán kính đáy là $r$ , chiều cao $h$ . Thể tích $V$ của khối nón đó là:

• A. $V = \pi {r^2}h$
• B. $V = \frac{1}{3}{r^2}h$
• C. $V = {r^2}h$
• D. $V = \frac{1}{3}\pi {r^2}h$

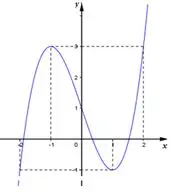
Câu 47: Đường cong ở hình bên dưới là đồ thị của một trong bốn hàm số dưới đây. Hàm số đó là hàm số nào ?

• A. $y = {x^3} - 3{x^2} + 1$
• B. $y = - {x^3} + 3{x^2} + 1$
• C. $y = {x^4} - 2{x^3} + 1$
• D. $y = {x^3} - 3x + 1$

Câu 48: Một khối trụ có thiết diện qua một trục là một hình vuông. Biết diện tích xung quanh của khối trụ bằng $16\pi $. Thể tích $V$ của khối trụ bằng:

• A. $V = 8\pi $
• B. $V = 16\pi $
• C. $V = 64\pi $
• D. $V = 32\pi $

Câu 49: Với $a$ và $b$ là hai số thực dương, $a \ne 1.$ Giá trị của ${a^{{{\log }_a}{b^3}}}$ bằng:

• A. $3b$
• B. ${b^3}$
• C. ${b^{\frac{1}{3}}}$
• D. $\frac{1}{3}b$

Câu 50: Cho biết hàm số $f\left( x \right)$ có đạo hàm $f'\left( x \right)$ và có một nguyên hàm là $F\left( x \right).$ Tìm $\int {\left[ {2f\left( x \right) + f'\left( x \right) + 1} \right]dx?} $

• A. $I = 2F\left( x \right) + f\left( x \right) + x + C$
• B. $I = 2xF\left( x \right) + f\left( x \right) + x + C$
• C. $I = 2xF\left( x \right) + x + 1$
• D. $I = 2F\left( x \right) + xf\left( x \right) + C$