Đề thi thử THPT quốc gia môn Vật Lý năm 2024 online – Mã đề 011

Câu 1: Trong con lắc lò xo nếu ta tăng khối lượng vật nặng lên $4$ lần và độ cứng tăng $2$ lần thì tần số dao động của vật:

• A. Tăng $2$ lần.
• B. Giảm $2$ lần.
• C. Tăng lần.
• D. Giảm lần.

Câu 2: Một vật dao động điều hòa có phương trình $x = 2cos\left( {2\pi t - \frac{{7\pi }}{6}} \right){\rm{ }}cm$. Li độ của vật tại thời điểm t = 0,25 (s) là:

• A. 1cm
• B. 1,5cm
• C. 0,5cm
• D. -1cm

Câu 3: Công suất của một đoạn mạch R, L, C nối tiếp không phụ thuộc vào:

• A. Độ tự cảm L của mạch điện.
• B. Pha ban đầu $\varphi $ của dòng điện qua mạch.
• C. Chu kì T của điện áp hai đầu đoạn mạch
• D. Dung kháng ZC của mạch điện.

Câu 4: Cho biết công thoát của Kali là $A{\text{ }} = {\text{ }}3,{6.10^{ - 19}}J$ . Chiếu vào Kali lần lượt bốn bức xạ ${\lambda _1} = 0,4\mu m;{\text{ }}{\lambda _2} = 0,5\mu m{\text{ }};{\text{ }}{\lambda _3} = 0,6\mu m;{\text{ }}{\lambda _4} = 0,7\mu m$ . Những bức xạ nào có thể gây ra hiện tượng quang điện đối với Kali?

• A. ${\lambda _3}$ và ${\lambda _4}$
• B. ${\lambda _1}$ và ${\lambda _2}$
• C. chỉ có ${\lambda _1}$
• D. ${\lambda _1},{\lambda _2}$ và ${\lambda _3}$

Câu 5: Biểu thức nào sau đây xác định cảm ứng từ của dòng điện thẳng dài đặt trong không khí:

• A. $B = {2.10^{ - 7}}{\rm{I}}{\rm{.r}}$
• B. $B = {2.10^{ - 7}}\frac{I}{r}$
• C. $B = {2.10^{ 7}}\frac{I}{r}$
• D. $B = {2.10^{ 7}}{\rm{I}}{\rm{.r}}$

Câu 6: Cho phương trình phản ứng: $_{92}^{238}U + n \to _Z^AX + _{18}^{37}{\rm{Ar}}$. Trong đó Z, A là:

• A. Z = 58, A = 143
• B. Z = 74, A = 202
• C. Z = 58, A = 139
• D. Z = 44, A = 140

Câu 7: Pin quang điện hoạt động dựa vào.

• A. Hiện tượng quang điện ngoài.
• B. Hiện tượng quang điện trong.
• C. Hiện tượng tán sắc ánh sáng.
• D. Sự phát quang của các chất

Câu 8: Biểu thức nào sau đây xác định vị trí các cực đại giao thoa với 2 nguồn cùng pha?

• A. ${d_2} - {d_1} = \left( {k + \frac{1}{2}} \right)\lambda $
• B. ${d_2} - {d_1} = \frac{{k\lambda }}{2}$
• C. ${d_2} - {d_1} = k\lambda $
• D. ${d_2} - {d_1} = \left( {k - \frac{1}{2}} \right)\lambda $

Câu 9: Tại một điểm trên mặt chất lỏng có một nguồn dao động với tần số 120 Hz, tạo ra sóng ổn định trên mặt chất lỏng. Xét 5 gợn lồi liên tiếp trên một phương truyền sóng ở về một phía so với nguồn, gợn thứ nhất cách gợn thứ năm 0,5m. Tính tốc độ truyền sóng trên mặt chất lỏng:

• A. 10 m/s
• B. 12 m/s
• C. 15 m/s
• D. 20 m/s

Câu 10: Mạch dao động điện từ gồm tụ điện C và cuộn cảm L, dao động tự do với tần số góc

• A. $\omega = 2\pi \sqrt {LC} $
• B. $\omega = \frac{{2\pi }}{{\sqrt {LC} }}$
• C. $\omega = \sqrt {LC} $
• D. $\omega = \frac{1}{{\sqrt {LC} }}$

Câu 11: Khi dùng kính lúp quan sát các vật nhỏ. Gọi α và αo lần lượt là góc trông của ảnh qua kính và góc trông trực tiếp vật khi đặt vật ở điểm cực cận của mắt. Số bội giác của mắt được tính theo công thức nào sau đây?

• A. $G = \frac{{tan\alpha }}{{tan{\alpha _0}}}$
• B. $G = \frac{{tan{\alpha _0}}}{{tan\alpha }}$
• C. $G = \frac{{{\rm{cos}}\alpha }}{{{\rm{cos}}{\alpha _0}}}$
• D. $G = \frac{{cos{\alpha _0}}}{{cos\alpha }}$

Câu 12: Một vật dao động tắt dần có các đại lượng giảm liên tục theo thời gian là

• A. Biên độ và gia tốc
• B. Li độ và tốc độ
• C. Biên độ và năng lượng
• D. Biên độ và tốc độ

Câu 13: Trong thí nghiệm Y-âng về giao thoa ánh sáng, khoảng cách giữa hai khe là a, khoảng cách từ mặt phẳng chứa hai khe đến màn quan sát là D. Khi nguồn sóng phát bức xạ đơn sắc có bước sóng λ thì khoảng vân giao thoa trên màn là i. Hệ thức nào sau đây đúng?

• A. i = $\frac{{\lambda a}}{D}$
• B. i = $\frac{{\lambda D}}{2a}$
• C. $\lambda $=$\frac{{ia}}{D}$
• D. $\lambda $=$\frac{i}{{aD}}$

Câu 14: Trong nghiên cứu phổ vạch của một vật bị kích thích phát quang dựa vào vị trí của các vạch, người ta biết:

• A. Nhiệt độ của vật đó.
• B. Các hợp chất hóa học tồn tại trong vật đó.
• C. Phương pháp kích thích vật dẫn đến phát quang.
• D. Các nguyên tố hóa học cấu thành vật đó

Câu 15: Mạch điện xoay chiều chỉ có tụ điện với điện dung C. Đặt vào hai đầu tụ điện một điện áp u = U0cos(ωt + $\varphi $) V. Cường độ dòng điện hiệu dụng của mạch được cho bởi công thức:

• A. $I = \dfrac{{{U_0}}}{{\sqrt 2 \omega C}}$
• B. $I = \dfrac{{{U_0}\omega C}}{{\sqrt 2 }}$
• C. $I = \dfrac{{{U_0}}}{{\omega C}}$
• D. $I = {U_0}\omega C$

Câu 16: Nếu quy ước: 1- chọn sóng; 2- tách sóng; 3- khuyếch đại âm tần; 4- khuyếch đại cao tần; 5-chuyển thành sóng âm. Việc thu sóng điện từ trong máy thu thanh phải qua các giai đoạn nào, với thứ tự nào?

• A. 1, 2, 5, 4, 3.
• B. 1, 3, 2, 4, 5.
• C. 1, 4, 2, 3, 5.
• D. 1, 2, 3, 4, 5.

Câu 17: Kết luận nào sau đây là sai ?

• A. Tia hồng ngoại và tử ngoại có thể dùng để sấy sản phẩm nông nghiệp, tia X có thể dùng để kiểm tra các khuyết tật của sản phẩm công nghiệp.
• B. Quang phổ liên tục phụ thuộc nhiệt độ của nguồn phát, quang phổ vạch phát xạ phụ thuộc thành phần cấu tạo của nguồn phát.
• C. Người ta thường dùng tia hồng ngoại để điều khiển từ xa các thiết bị điện tử.
• D. Tia tử ngoại bị nước hấp thụ mạnh.

Câu 18: Dao động điện từ nào dưới đây xảy ra trong một mạch dao động có thể có biên độ giảm dần theo thời gian?

• A. Dao động điện từ duy trì.
• B. Dao động điện từ không lí tưởng.
• C. Dao động điện từ riêng.
• D. Dao động điện từ cộng hưởng.

Câu 19: Một vật dao động điều hòa với tần số 5 Hz và biên độ 8 cm. Chọn gốc thời gian lúc vật qua vị trí cân bằng theo chiều âm. Phương trình dao động của là:

• A. x = 4cos(10 π t – π/2) cm.
• B. x = 4cos(10t + π/2) cm.
• C. x = 8cos(10 π t + π/2) cm.
• D. x = 8cos(10t – π/2) cm.

Câu 20: Một vật dao động điều hoà với phương trình $x = 8cos\left( {2\pi t - \dfrac{\pi }{3}} \right)cm$. Tìm số lần vật qua vị trí có độ lớn vận tốc $8\pi \left( {cm/s} \right)$ trong thời gian $\dfrac{{35}}{6}s$ tính từ thời điểm gốc.

• A. 24 lần
• B. 11 lần
• C. 12 lần
• D. 23 lần

Câu 21: Con lắc đơn có chiều dài dây treo là l = 1 m thực hiện 10 dao động mất 20s. Lấy π = 3,14 . Gia tốc trọng trường tại nơi đặt con lắc là:

• A. g $ \approx $ 10 m/s2
• B. g $ \approx $ 9, 75 m/s2
• C. g $ \approx $ 9,95 m/s2
• D. g $ \approx $ 9,86 m/s2

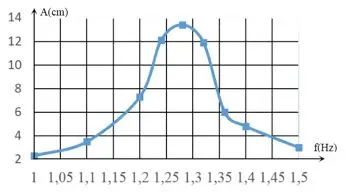
Câu 22: Khảo sát thực nghiệm một con lắc lò xo gồm vật nhỏ có khối lượng $216{\rm{ }}g$ và lò xo có độ cứng k, dao động dưới tác dụng của ngoại lực $F{\rm{ }} = {\rm{ }}{F_0}cos2\pi ft$, với ${F_0}$ không đổi và $f$ thay đổi được. Kết quả khảo sát ta được đường biểu diễn biên độ $A$ của con lắc theo tần số $f$ có đồ thị như hình vẽ. Giá trị của $k$ xấp xỉ bằng:

• A. $13,64{\rm{ }}N/m$
• B. $12,35{\rm{ }}N/m$
• C. $15,64{\rm{ }}N/m$
• D. $16,71{\rm{ }}N/m$

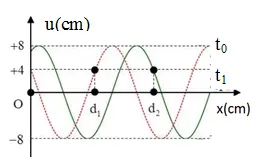
Câu 23: Một sóng cơ truyền trên trục Ox trên một dây đàn hồi rất dài với tần số f = 1/3 Hz. Tại thời điểm t0 = 0 và tại thời điểm t1 = 0,875s hình ảnh của sợi dây được mô tả như hình vẽ. Biết rằng: d2 - d­1 = 10 cm. Gọi δ là tỉ số giữa tốc độ dao động cực đại của phần tử trên dây và tốc độ truyền sóng. Giá trị của δ là:

• A. π
• B. $\dfrac{{3\pi }}{5}$
• C. $\dfrac{{5\pi }}{3}$
• D. 2π

Câu 24: Quan sát sóng dừng trên một sợi dây đàn hồi, người ta đo được khoảng cách giữa 5 nút sóng liên tiếp là 100 cm. Biết tần số của sóng truyền trên dây bằng 100 Hz, vận tốc truyền sóng trên dây là:

• A. 50 m/s
• B. 100 m/s
• C. 25 m/s
• D. 75 m/s

Câu 25: Có một số nguồn âm giống nhau với công suất phát âm không đổi trong môi trường đẳng hướng không hấp thụ âm. Nếu tại điểm A đặt 4 nguồn âm thì tại điểm B cách A một đoạn d có mức cường độ âm là 60dB. Nếu tại điểm C cách B một đoạn 2d/3 đặt 6 nguồn âm thì tại điểm B có mức cường độ âm bằng:

• A. 58,42dB
• B. 65,28dB
• C. 54,72dB
• D. 61,76dB

Câu 26: Tại thời điểm t, điện áp $u = 200\sqrt 2 {\text{cos}}\left( {100\pi t - \dfrac{\pi }{2}} \right)$ (trong đó u tính bằng V, t tính bằng s) có giá trị $100\sqrt 2 $ và đang giảm. Sau thời điểm đó $\dfrac{1}{{300}}s$, điện áp này có giá trị là:

• A. $-100V$
• B. $ 100\sqrt 3 V$
• C. $ - 100\sqrt 2 V$
• D. $200V$

Câu 27: Đoạn mạch RLC nối tiếp $R = 40\Omega $; $L = \dfrac{{0,4}}{\pi }(H)$ và $C = \dfrac{{{{10}^{ - 3}}}}{\pi }(F)$. Cho tần số dòng điện là 50 Hz và điện áp hiệu dụng ở hai đầu R là 80 V. Điện áp ở hai đầu đoạn mạch là:

• A. 100 V
• B. 150 V
• C. 200 V
• D. 50 V

Câu 28: Đặt điện áp xoay chiều có giá trị hiệu dụng và tần số không đổi vào hai đầu đoạn mạch gồm biến trở R mắc nối tiếp với tụ điện có điện dung C. Gọi điện áp hiệu dụng giữa hai đầu tu điện, giữa hai đầu biến trở và hệ số công suất của đoạn mạch khi biến trở có giá trị R1 lần lượt là ${U_{C1}},{\rm{ }}{U_{R1}}$ và $cos{\varphi _1}$ ; khi biến trở có giá trị R2 thì các giá trị tương ứng nói trên là ${U_{C2}},{\rm{ }}{U_{R2}}$ và $cos{\varphi _2}$. Biết ${U_{C1}} = {\rm{ }}2{U_{C2}},{\rm{ }}{U_{R2}} = {\rm{ }}2{U_{R1}}.$ Giá trị của $cos{\varphi _1}$ và $cos{\varphi _2}$ là:

• A. $\cos {\varphi _1} = \dfrac{1}{{\sqrt 3 }},\,\cos {\varphi _2} = \dfrac{2}{{\sqrt 5 }}$.
• B. $\cos {\varphi _1} = \dfrac{1}{{\sqrt 5 }},\,\cos {\varphi _2} = \dfrac{1}{{\sqrt 3 }}$.
• C. $\cos {\varphi _1} = \dfrac{1}{{\sqrt 5 }},\,\cos {\varphi _2} = \dfrac{2}{{\sqrt 5 }}$.
• D. $\cos {\varphi _1} = \dfrac{1}{{2\sqrt 2 }},\,\cos {\varphi _2} = \dfrac{1}{{\sqrt 2 }}$.

Câu 29: Trên đoạn mạch xoay chiều không phân nhánh có bốn điểm theo đúng thứ tự A, M, N, B. Giữa hai điểm A và M chỉ có cuộn cảm thuần, giữa hai điểm M và N chỉ có điện trở thuần, giữa hai điểm N và B chỉ có tụ điện. Điện áp hiệu dụng giữa hai điểm A và M là 150V và điện áp hiệu dụng giữa hai điểm N và B là 200/3 V. Điện áp tức thười trên đoạn AN và trên đoạn MB lệch pha nhau 900. Điện áp hiệu dụng trên R là:

• A. 100 V
• B. 120 V
• C. 90 V
• D. 180 V

Câu 30: Mạch chọn sóng của một máy thu thanh gồm cuộn dây có độ tự cảm L = 2.10-6 H, điện trở thuần R = 0. Để máy thu thanh chỉ có thể thu được các sóng điện từ có bước sóng từ 57m đến 753m, người ta mắc tụ điện trong mạch trên bằng một tụ điện có điện dung biến thiên. Hỏi tụ điện này phải có điện dung trong khoảng nào?

• A. 2,05.10-7F ≤ C ≤ 14,36.10-7F
• B. 0,45.10-9F ≤ C ≤ 79,7.10-9F
• C. 3,91.10-10F ≤ C ≤ 60,3.10-10F
• D. 0,12.10-8F ≤ C ≤ 26,4.10-8F

Câu 31: Trong thí nghiệm Y-âng về giao thoa ánh sáng, các khe hẹp được chiếu sáng bởi ánh sáng đơn sắc. Khoảng vân trên màn là 1,5mm. Trong khoảng giữa hai điểm N và M trên màn ở cùng một phía so với vân sáng trung tâm, cách vân trung tâm lần lượt 2,2 mm và 4,7 mm, quan sát được:

• A. 2 vân sáng và 2 vân tối.
• B. 3 vân sáng và 2 vân tối.
• C. 2 vân sáng và 3 vân tối
• D. 2 vân sáng và 1 vân tối.

Câu 32: Trong một đèn huỳnh quang, ánh sáng kích thích có bước sóng $0,36\mu m$ thì photon ánh sáng huỳnh quang có thể mang năng lượng là?

• A. 5 eV
• B. 3 eV
• C. 4 eV
• D. 6 eV

Câu 33: Khi êlectrôn trong nguyên tử hiđrô chuyển từ quĩ đạo dừng có năng lượng -0,85 eV sang quĩ đạo dừng có năng lượng -13,60 eV thì nguyên tử phát bức xạ điện từ có bước sóng:

• A. $0,4340{\rm{ }}\mu m$
• B. $0,4860{\rm{ }}\mu m$
• C. $0,0974{\rm{ }}\mu m$
• D. $0,6563{\rm{ }}\mu m$

Câu 34: Các hạt nhân Đơteri $_1^2H$, Triti $_1^3H$, Heli $_2^4He$ có năng lượng liên kết lần lượt là 2,22 MeV, 8,49 MeV và 28,16 MeV. Các hạt nhân trên được sắp xếp theo thứ tự giảm dần về độ bền vững của hạt nhân 1à:

• A. $_1^2H$;$_2^4He$; $_1^3H$
• B. $_1^2H$; $_1^3H$;$_2^4He$
• C. $_2^4He$; $_1^3H$;$_1^2H$
• D. $_1^3H$;$_2^4He$; $_1^2H$

Câu 35: Tính số hạt nhân bị phân rã sau 1s trong 1g Rađi ${}^{226}$Ra . Cho biết chu kỳ bán rã của ${}^{226}$Ra là 1580 năm. Số Avôgađrô là NA = 6,02.1023 mol-1.

• A. 3,55.1010 hạt
• B. 3,40.1010 hạt
• C. 3,75.1010 hạt
• D. 3,70.1010 hạt

Câu 36: Một vật sáng AB cho ảnh thật qua một thấu kính hội tụ, ảnh này hứng trên một màn E đặt cách vật một khoảng 180cm, ảnh thu được cao bằng 1/5 vật. Tiêu cự của thấu kính có giá trị:

• A. 15cm
• B. 10cm
• C. 5cm
• D. 25cm

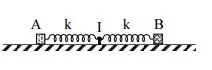
Câu 37: Trên mặt phẳng nằm ngang có hai con lắc lò xo. Các lò xo có cùng độ cứng k, cùng chiều dài tự nhiên là 32 cm. Các vật nhỏ A và B có khối lượng lần lượt là m và 4m. Ban đầu, A và B được giữ ở vị trí sao cho lò xo gắn với A bị dãn 8 cm còn lò xo gắn với B bị nén 8 cm. Đồng thời thả nhẹ để hai vật dao động điều hòa trên cùng một đường thẳng đi qua giá I cố định (hình vẽ). Trong quá trình dao động, khoảng cách lớn nhất và nhỏ nhất giữa hai vật có giá trị lần lượt là

• A. 64 cm và 48 cm
• B. 80 cm và 48 cm
• C. 64 cm và 55 cm
• D. 80 cm và 55 cm

Câu 38: Trên đoạn mạch xoay chiều không phân nhánh có 4 điểm theo đúng thứ tự A, M, N và B. Giữa hai điểm A và M chỉ có cuộn dây, giữa 2 điểm M và N chỉ có điện trở thuần, giữa 2 điểm N và B chỉ có tụ điện. Điện áp hiệu dụng giữa 2 điểm A và N là 60 V và điện áp hiệu dụng giữa 2 điểm M và B là $40\sqrt 3 V$ . Điện áp tức thời trên đoạn AN và trên đoạn MB lệch pha nhau 900, điện áp tức thời trên đoạn MB và trên đoạn NB lệch pha nhau 300 và cường độ hiệu dụng trong mạch là $\sqrt 3 A$. Điện trở thuần của cuộn dây là:

• A. $40 Ω$
• B. $10 Ω$
• C. $50 Ω$
• D. $20 Ω$

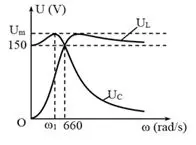
Câu 39: Cho mạch điện xoay chiều gồm một điện trở thuần, cuộn cảm thuần và tụ điện mắc nối tiếp theo thứ tự trên. Đặt vào hai đầu đoạn mạch điện áp xoay chiều có giá trị hiệu dụng không đổi có tần số góc $\omega $ thay đổi được. Đồ thị biểu diễn sự phụ thuộc vào tần số góc $\omega $ của điện áp hiệu dụng giữa hai bản tụ và hai đầu cuộn cảm lần lượt là ${U_C},{U_L}$ như hình vẽ dưới. Khi $\omega = {\omega _1}$ thì điện áp hiệu dụng giữa hai bản tụ ${U_C}$ cực đại là ${U_m}$. Giá trị của ${U_m}$ là:

• A. $150\sqrt 3 V$
• B. $100\sqrt 3 V$
• C. $200\sqrt 3 V$
• D. $150\sqrt 2 V$

Câu 40: Dùng prôtôn bắn vào hạt nhân ${}_{\rm{4}}^{\rm{9}}{\rm{Be}}$ đứng yên, sau phản ứng sinh ra hạt α và hạt nhân X có động năng lần lượt là Kα = 3,575 MeV và KX = 3,150 MeV. Phản ứng này tỏa ra năng lượng bằng ΔE = 2,125 MeV. Coi khối lượng các hạt nhân tỉ lệ với số khối của nó. Góc hợp giữa các hướng chuyển động của hạt α và hạt prôtôn là

• A. φ = 60o
• B. φ = 90o
• C. φ = 75o
• D. φ = 45o