Đề thi thử THPT QG năm 2021 môn Vật Lý online – Đề thi của Trường THPT Lê Văn Đẩu giúp bạn luyện tập thường xuyên để ghi nhớ lâu hơn thông qua các câu hỏi được chọn lọc kỹ lưỡng. Các câu hỏi được phân bổ hợp lý theo mức độ nhận thức giúp bạn không bị quá tải. Đặc biệt phù hợp với người chuẩn bị cho các kỳ kiểm tra quan trọng. Thông qua quá trình làm bài, bạn có thể biết được nội dung nào cần ôn lại. Điều này giúp việc học trở nên hiệu quả hơn.
Đề thi thử THPT QG năm 2021 môn Vật Lý online – Đề thi của Trường THPT Lê Văn Đẩu
Câu 1: Tia nào sau đây được dùng để nghiên cứu thành phần và cấu trúc của các vật rắn?
Câu 2: Ở một đường sức của một điện trường đều có hai điểm M và N cách nhau 40 cm. Hiệu điện thế giữa M và N là 80V. Cường độ điện trường có độ lớn là
Câu 3: Trong đoạn mạch xoay chiều gồm điện trở thuần, cuộn dây và tụ điện mắc nối tiếp, nếu tần số của dòng điện tăng thì
Câu 4: Một điểm trong không gian có sóng điện từ truyền qua, thì tại đó
Câu 5: Bước sóng là khoảng cách giữa hai phần tử sóng
Câu 6: Chọn câu đúng. Theo thuyết lượng tử ánh sáng thì năng lượng của
Câu 7: Trong nguyên tắc của việc thông tin liên lạc bằng sóng vô tuyến, để trộn dao động âm tần với dao động cao tần ta dùng
Câu 8: Đơn vị của khối lượng nguyên tử u là
Câu 9: Chiếu một chùm sáng đi qua một máy quang phổ lăng kính, chùm sáng đi qua
Câu 10: Gọi ${{m}_{p}}$, ${{m}_{n}}$, ${{m}_{x}}$ lần lượt là khối lượng của prôtôn, nơtron và hạt nhân $_{X}^{A}X$. Năng lượng liên kết của một hạt nhân $_{X}^{A}X$ được xác định bởi công thức:
Câu 11: Một con lắc lò xo gồm vật nhỏ có khối lượng m và lò xo nhẹ có độ cứng k. Con lắc dao động điều hòa với tần số góc:
Câu 12: Trong quá trình truyền tải điện năng đi xa, để giảm công suất hao phí trên dây truyền tải n lần thì người ta thường sử dụng biện pháp nào sau đây?
Câu 13: Chọn câu đúng. Quang phổ vạch hấp thụ là
Câu 14: Một vật dao động điều hòa theo phương trình $x=A\cos \left( \omega t+\varphi \right)$. Gia tốc của vật được tính bằng công thức
Câu 15: Dòng điện xoay chiều sử dụng trong gia. đình có thông số 200 V - 50 Hz. Nếu sử dụng dòng điện trên để thắp sáng bóng đèn sợi đốt 220 V - 100 W thì trong mỗi giây đèn sẽ
Câu 16: Chỉ ra câu sai. Âm La của một cái đàn ghita và của một cái kèn có thể cùng:
Câu 17: Đặt một điện áp $u={{U}_{0}}\cos \left( \omega t+\frac{\pi }{4} \right)$ vào hai đầu đoạn mạch chỉ có tụ điện thì cường độ dòng điện trong mạch là $i={{I}_{0}}\cos \left( \omega t+\varphi \right)$. Giá trị của $\varphi $ bằng:
Câu 18: Một con lắc lò xo dao động điều hoà khỉ vật đi qua vị trí có li độ bằng nửa biên độ thì
Câu 19: Đặt vào hai đầu đoạn mạch R, L, C mắc nối tiếp, với cuộn dây thuần cảm, một điện áp $u=220\cos \left( 100\pi t-\frac{\pi }{3} \right)$ V. Biết $R=100\Omega $, $L=\frac{2}{\pi }H$, $C=\frac{1}{10\pi }$ mF. Biểu thức cường độ dòng điện trong mạch là:
Câu 20: Công suất của một nguồn sáng là $P=2,5W$. Biết nguồn phát ra ánh sáng đơn sắc có bước sóng $\lambda =0,3\mu m$. Cho hằng số Plăng là $6,{{625.10}^{-34}}$J.s và tốc độ ánh sáng trong chân không ${{3.10}^{8}}$ m/s. số phôtôn phát ra từ nguồn sáng trong một phút là
Câu 21: Một mạch dao động lí tưởng gồm cuộn cảm thuần có độ tự cảm 5 mH và tụ điện có điện dung $50\mu F$. Trong mạch đang có dao động điện từ tự do với hiệu điện thế cực đại giữa hai bản tụ điện là 6 V. Tại thời điểm hiệu điện thế giữa hai bản tụ điện là 4 V thì cường độ dòng điện trong mạch có độ lớn bằng:
Câu 22: Cho bốn bức xạ điện từ có bước sóng ${{\lambda }_{1}}=0,2\,\mu m$, ${{\lambda }_{2}}=0,3\,\mu m$, ${{\lambda }_{3}}=0,4\,\mu m$ và ${{\lambda }_{4}}=0,6\,\mu m$. Chiếu lần lượt 4 bức xạ trên vào một tấm kẽm có công thoát $A=3,55eV$. Số bức xạ gây ra hiệu ứng quang điện ngoài đối với tấm kẽm là
Câu 23: Trong thí nghiệm Y-âng về giao thoa ánh sáng, chiếu sáng các khe bằng bức xạ có bước sóng 600 nm. Khoảng cách giữa hai khe là 1 mm, khoảng cách từ mặt phẳng hai khe đến màn quan sát là 2 m. Trên màn, tại điểm M cách vân trung tâm 2,4 mm có:
Câu 24: Một mạch điện kín gồm nguồn điện $E=12V$, $r=1\Omega $. Mạch ngoài gồm bóng đèn có ghi (6V - 6W) mắc nối tiếp với một biến trở. Để đèn sáng bình thường, biến trở có giá trị bằng
Câu 25: Hai dao động điều hòa cùng phương có phương trình lần lượt là ${{x}_{1}}=6\cos \left( \omega t+\frac{\pi }{3} \right)\left( cm \right)$ và ${{x}_{2}}=8\cos \left( \omega t-\frac{\pi }{6} \right)\left( cm \right)$. Dao động tổng hợp có biên độ là
Câu 26: Cho biết khối lượng hạt proton là ${{m}_{p}}=1,0073\,u$, của nơtron là ${{m}_{n}}=1,0087\,u$ và của hạt nhân $_{2}^{4}He$ là ${{m}_{\alpha }}=4,0015\,u$ và $1u{{c}^{2}}=931,5\,MeV$. Năng lượng liên kết tính riêng cho từng nuclôn của hạt nhân $_{2}^{4}He$ là
Câu 27: Một con lắc lò xo gồm lò xo có độ cứng 40 N/m và vật nhỏ có khối lượng m. Tác dụng lên vật một ngoại lực $F=5\cos 10t\left( N \right)$ (t tính bằng s) dọc theo trục lò xo thì xảy ra hiện tượng cộng hưởng. Lấy ${{\pi }^{2}}=10$. Giá trị của m bằng
Câu 28: Trong thí nghiệm Y-âng về giao thoa ánh sáng, khoảng cách giữa hai khe là 2 mm, khoảng cách từ hai khe đến màn là 2 m. Nguồn S phát ánh sáng trắng có bước sóng từ $0,38\,\mu m$ đến $0,76\,\mu m$. Vùng phủ nhau giữa quang phổ bậc 2 và bậc 3 có bề rộng là:
Câu 29: Một sóng cơ truyền dọc theo trục Ox có phương trình $u=9\cos \left( 2\pi t-4\pi x \right)$ (trong đó x tính bằng mét và t tính bằng giây). Tốc độ truyền sóng bằng:
Câu 30: Một đường dây tải điện có công suất hao phí trên đường dây là 500 W. Sau đó người ta mắc thêm vào mạch một tụ điện sao cho công suất hao phí giảm đến giá trị cực tiểu và bằng 320 W (công suất và điện áp truyền đi không đổi). Hệ số công suất của mạch điện lúc đầu là
Câu 31: Một vật dao động điều hòa với chu kì $T=1$ s và biên độ $A=10$ cm. Tốc độ trung bình lớn nhất của vật thực hiện được trong khoảng thời gian $\frac{2}{3}$ s là:
Câu 32: Một tia sáng truyền từ không khí vào môi trường thủy tinh có chiết suất tuyệt đối $n=\sqrt{3}$ dưới góc tới 60°, coi không khí có chiết suất tuyệt đối là 1. Góc khúc xạ có giá trị là
Câu 33: Chiếu bức xạ có bước sóng $\lambda =0,405\,\mu m$vào một tấm kim loại thì vận tốc ban đầu cực đại của electron là ${{v}_{1}}$, thay bức xạ khác có tần số ${{f}_{2}}={{16.10}^{14}}Hz$ thì vận tốc ban đầu cực đại của electron là ${{v}_{2}}=2{{v}_{1}}$. Công thoát của electron ra khỏi kim loại đó bằng bao nhiêu?
Câu 34: Cho phản ứng hạt nhân: $_{11}^{23}Na+_{1}^{1}H\to _{2}^{4}He+_{10}^{20}Ne$. Lấy khối lượng các hạt nhân $_{11}^{23}Na$; $_{10}^{20}Ne$; $_{2}^{4}He$; $_{1}^{1}H$ lần lượt là 22,9837 u; 19,9869 u; 4,0015 u; 1,0073 u và $1\,u=931,5\,MeV/{{c}^{2}}$. Trong phản ứng này, năng lượng
Câu 35: Mạch chọn sóng của máy thu vô tuyến gồm tụ xoay C và cuộn thuần cảm L. Tụ xoay có điện dung C tỉ lệ theo hàm bậc nhất đối với góc xoay $\alpha $. Ban đầu khi chưa xoay tụ thì mạch thu được sóng có tần số ${{f}_{0}}$. Khi xoay tụ một góc ${{\alpha }_{1}}$ thì mạch thu được sóng có tần số ${{f}_{1}}=0,5{{f}_{0}}$, khi tụ xoay góc ${{\alpha }_{2}}$ thì mạch thu được sóng có tần số ${{f}_{2}}=\frac{{{f}_{0}}}{3}$. Tỉ số giữa hai góc xoay $\frac{{{\alpha }_{1}}}{{{\alpha }_{2}}}$ là:
Câu 36: Một electron bay vào không gian có từ trường đều B với vận tốc ban đầu $\overrightarrow{{{v}_{0}}}$ vuông góc cảm ứng từ. Quỹ đạo của electron trong từ trường là một đường tròn có bán kính R. Khi tăng độ lớn của cảm úng từ lên gấp đôi thì:
Câu 37: Tốc độ truyền âm trong không khí là 330m/s, trong nước là 1435m/s. Một âm có bước sóng trong không khí là 50 cm thì khi truyền trong nước có bước sóng là
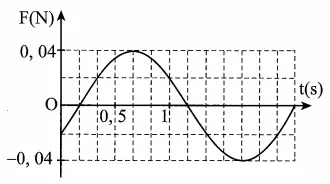
Câu 38: Một vật có khối lượng $m=100$ g, dao động điều hoà dọc theo trục Ox. Hình bên là đồ thị biểu diễn sự phụ thuộc của lực kéo về F theo thời gian t. Biên độ dao động của vật là
Câu 39: Trong thí nghiệm Y-âng về giao thoa với ánh sáng đơn sắc, khoảng cách từ mặt phẳng chứa hai khe đến màn quan sát là 1,5 m. Trên màn quan sát, hai điểm M và N đối xứng qua vân trung tâm có hai vân sáng bậc 4. Dịch màn ra xa khe thêm một đoạn 50 cm theo phương vuông góc với mặt phẳng chứa hai khe. So với lúc chưa dịch chuyển màn, số vân sáng trên đoạn MN lúc này giảm đi:
Câu 40: Trên mặt nước có hai nguồn sóng kết hợp A, B cách nhau 68 mm, dao động điều hòa cùng tần số, cùng pha theo phương vuông góc với mặt nước, bước sóng 10 mm. Điểm C là trung điểm của AB. Trên đường tròn tâm C bán kính 20 mm nằm trên mặt nước có bao nhiêu điểm dao động với biên độ cực đại: