Đề thi thử THPT QG năm 2022 môn Vật Lý online – Đề thi của Trường THPT Tôn Đức Thắng giúp bạn nhận biết điểm mạnh và điểm yếu của bản thân thông qua dạng bài tập quen thuộc thường gặp trong đề thi. Các câu hỏi được xây dựng theo lộ trình giúp bạn tự tin hoàn thành bài quiz. Đặc biệt phù hợp với người học muốn tự đánh giá năng lực. Thông qua quá trình làm bài, bạn có thể điều chỉnh phương pháp học tập cho phù hợp. Điều này giúp việc học trở nên tiết kiệm thời gian hơn.
Đề thi thử THPT QG năm 2022 môn Vật Lý online – Đề thi của Trường THPT Tôn Đức Thắng
Câu 1: Một chất điểm M có khối ượng m = 20g dao động điều hòa, một phần đồ thị của lực kéo về theo thời gian có dạng như hình vẽ, lấy ${{\pi }^{2}}\approx 10$. Dựa vào đồ thị suy ra phương trình dao động của chất điểm là

Câu 2: Một chất điểm tham gia đồng thời hai dao động điều hòa, cùng phương, cùng tần số với các biên độ là $6 \mathrm{~cm}$ và $4 \mathrm{~cm}$. Tại thời điểm t, các dao động có li độ lần lượt là $\mathrm{x}_{1}$ và $\mathrm{x}_{2}$. Biết rằng giá trị cực đại của $\mathrm{x}_{1} \mathrm{x}_{2}$ là D, giá trị cực tiểu của $\mathrm{x}_{1} \mathrm{x}_{2}$ là $\frac{-\mathrm{D}}{3}$. Biên độ dao động của vật gần nhất với giá trị nào sau đây?
Câu 3: Trong môi trường đẳng hướng và không hấp thụ âm, trên mặt phẳng nằm ngang có 3 điểm O, M, N tạo thành tam giác vuông tại O, với OM = 80 m, ON = 60 m. Đặt tại O một nguồn điểm phát âm công suất P không đổi thì mức cường độ âm tại M là 50 dB. Mức cường độ âm lớn nhất trên đoạn MN xấp xỉ bằng
Câu 4: Cuộn cảm của một mạch dao dộng có độ tự cảm $L=50$µH. Tụ điện của mạch có điện dung biến thiên được trong khoảng từ 60 pF – 240 pF. Tần số dao động riêng của mạch biến thiên trong khoảng từ
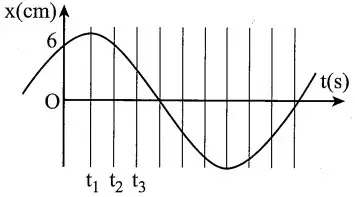
Câu 5: Một chất điểm dao động điều hòa có li độ phụ thuộc theo thời gian được biểu diễn như hình vẽ bên. Biết các khoảng chia từ ${{t}_{1}}$ trở đi bằng nhau nhưng không bằng khoảng chia từ 0 đến ${{t}_{1}}$. Quãng đường chất điểm đi được từ thời điểm ${{t}_{2}}$ đến thời điểm ${{t}_{3}}$ gấp 2 lần quãng đường chất điểm đi được từ thời điểm 0 đến thời điểm ${{t}_{1}}$ và ${{t}_{3}}-{{t}_{2}}=0,2\left( s \right)$. Độ lớn vận tốc của chất điểm tại thời điểm ${{t}_{3}}$ xấp xỉ bằng
Câu 6: Điện năng truyền từ một trạm phát điện với công suất 200kW. Số chỉ của các công tơ điện ở trạm phát và ở nơi tiêu thụ sau mỗi ngày đêm chênh lệch nhau 240kW.h. Hiệu suất của quá trình truyền tải là
Câu 7: Một máy biến áp lí tưởng có số vòng dây ở cuộn sơ cấp là 5000 vòng, số vòng dây ở cuộn thứ cấp là 250 vòng. Biết điện áp hiệu dụng ở hai đầu cuộn sơ cấp là 220 V. Điện áp hiệu dụng ở hai đầu cuộn thứ cấp là
Câu 8: Một sóng cơ lan truyền trên mặt thoáng một chất lỏng với tần số 10Hz, tốc độ truyền sóng là 1,2m/s. Hai điểm M,N thuộc mặt thoáng, trên cùng một phương truyền sóng, cách nhau 26cm (M gần nguồn hơn). Tại thời điểm t, điểm N hạ xuống thấp nhất. Khoảng thời gian ngắn nhất sau đó điểm M hạ xuống điểm thấp nhất là
Câu 9: Để phân loại sóng ngang và sóng dọc người ta dựa vào đâu?
Câu 10: Người ta đặt chìm trong nước một nguồn âm có tần số 725 Hz và vận tốc truyền âm trong nước là 1450 m/s. Khoảng cách giữa hai điểm gần nhau nhất trong nước và dao động ngược pha là?
Câu 11: Chuyển động của một vật là tổng hợp của hai dao động điều hòa cùng phương cùng tần số có các phương trình là x1 = 4cos(10t + π/4) cm; x2 = 3cos(10t + 3π/4) cm. Gia tốc cực đại của vật trong quá trình dao động là
Câu 12: Hai chất điểm M, N dao động điều hòa cùng tần số dọc theo hai đường thẳng song song kề nhau và song song với trục Ox. Vị trí cân bằng của M và N đều nằm trên một đường thẳng qua gốc tọa độ và vuông góc với trục Ox. Trong quá trình dao động, hình chiếu của M và N trên Ox cách xa nhau nhất là $\sqrt 2 $cm. Biên độ dao động tổng hợp của M và N là 2 cm. Gọi AM, AN lần lượt là biên độ của M và N. Giá trị lớn nhất của (AM + AN) gần với giá trị nào nhất sau đây?
Câu 13: Một chất điểm thực hiện đồng thời hai dao động điều hòa cùng phương cùng tần số . Nếu hai dao động thành phần lệch pha nhau $\frac{{\rm{\pi }}}{{\rm{2}}}$ thì biên độ dao động tổng hợp là 20 cm. Nếu hai dao động thành phần ngược pha thì biên độ dao động tổng hợp là 15,6 cm. Biết biên độ của dao động thành phần thứ nhất lớn hơn so với biên độ của dao động thành phần thứ 2. Hỏi nếu hai dao động thành phần trên cùng pha với nhau thì biên độ dao động tổng hợp có giá trị gần giá trị nào nhất sau đây?
Câu 14: Chất phóng xạ X có chu kỳ bán rã T1, chất phóng xạ Y có chu kỳ bán rã T2 =2T1. Trong cùng một khoảng thời gian, nếu chất phóng xạ Y có số hạt nhân còn lại bằng $\frac{1}{4}$ số hạt nhân Y ban đầu thì tỉ số giữa số hạt nhân X bị phân rã so với số hạt nhân X ban đầu là
Câu 15: Ban đầu một mẫu chất phóng xạ nguyên chất có hạt nhân. Biết chu kì bán rã của chất phóng xạ này là T. Sau thời gian 3T, kể từ thời điểm ban đầu, số hạt chưa phân rã của mẫu chất phóng xạ này là
Câu 16: Cho khối lượng của hạt proton, notron và hạt nhân Heli ( ${}_2^4He$ ) lần lượt là 1,0073u; 1,0087u và 4,0015u. Biết 1u = 931,5 $\left( {MeV/{c^2}} \right)$ . Năng lượng liên kết của hạt nhân ${}_2^4He$ xấp xỉ bằng
Câu 17: Số nơtron của hạt nhân ${}_{92}^{235}U$ nhiều hơn số nơtron của hạt nhân ${}_{82}^{206}Pb$ là
Câu 18: Mức năng lượng của nguyên tử hydro xác định theo biểu thức ${E_n} = \frac{{13,6}}{{{n^2}}}eV$ (với n = 1, 2, 3, …). Nguyên tử đang ở trạng thái cơ bản thì hấp thụ được một photon làm bán kính quỹ đạo dừng của electron tăng lên 9 lần. Bước sóng nhỏ nhất mà nguyên tử này có thể phát ra là
Câu 19: Trong nguyên tử hydro, khi electron chuyển động trên quỹ đạo N thì có tốc độ bằng (cho biết bán kính Bo r0 = 5,3.10-11m)
Câu 20: Trong hiện tượng quang – phát quang, nếu ánh sáng phát quang là ánh sáng màu lục thì ánh sáng kích thích không thể là ánh sáng nào sau đây?
Câu 21: Điện năng ở một nhà máy điện trước khi truyền đi xa phải đưa tới một máy tăng áp. Ban đầu, số vòng dây của cuộn thứ cấp ở máy tăng áp là thì hiệu suất của quá trình truyền tải là 80%. Giữ điện áp và số vòng dây ở cuộn sơ cấp không đổi. Để hiệu suất của quá trình truyền tải tăng lên đến 95% thì số vòng dây của cuộn thứ cấp ở máy biến áp phải là
Câu 22: Trong quá trình truyền tải điện năng đi xa, nếu điện áp truyền đi không đổi và hệ số công suất luôn bằng 1thì khi công suất giảm đi 2 lần sẽ làm cho hao phí trên dây
Câu 23: Một máy biến áp lí tưởng có số vòng dây ở cuộn sơ cấp là 5000 vòng, số vòng dây ở cuộn thứ cấp là 250 vòng. Biết điện áp hiệu dụng ở hai đầu cuộn sơ cấp là 220 V. Điện áp hiệu dụng ở hai đầu cuộn thứ cấp là
Câu 24: Một đường dây tải điện giữa hai địa điểm A và B có hệ số công suất bằng 1. Tại A đặt máy tăng áp, tại B đặt máy hạ áp. Đường dây tải điện có điện trở tổng cộng 20Ω. Cường độ hiệu dụng của dòng điện trên dây tải là 110A. Công suất hao phí trên đường dây tải bằng 5% công suất tiêu thụ ở B. Điện áp hiệu dụng giữa hai đầu cuộn thứ cấp của máy hạ áp là 220V. Ở máy hạ áp, tỉ số giữa số vòng dây cuộn sơ cấp và thứ cấp là
Câu 25: Điện năng được truyền từ nơi phát đến một khu dân cư bằng đường dây một pha với hiệu suất truyền tải là 90%. Coi hao phí điện năng chỉ do tỏa nhiệt trên đường dây và không vượt quá 20%. Nếu công suất sử dụng điện của khu dân cư này tăng 20% và giữ nguyên điện áp ở nơi phát thì hiệu suất truyền tải điện năng trên chính đường dây đó là
Câu 26: Người ta truyền một công suất 500 kW từ một trạm phát điện đến nơi tiêu thụ bằng đường dây một pha. Biết công suất hao phí trên đường dây là 10 kW, điện áp hiệu dụng ở trạm phát là 35 kV. Coi hệ số công suất của mạch truyền tải điện bằng 1. Điện trở tổng cộng của đường dây tải điện là
Câu 27: Một vật tham gia đồng thời hai dao động điều hòa cùng phương, cùng tần số, nhưng vuông pha nhau, có biên độ tương ứng là A1 và A2. Biết dao động tổng hợp có phương trình $x = 16\cos \omega t$ (cm) và lệch pha so với dao động thứ nhất một góc ${\alpha _1}$ . Thay đổi biên độ của hai dao động, trong đó biên độ của dao động thứ hai tăng lên $\sqrt {15} $ lần (nhưng vẫn giữ nguyên pha của hai dao động thành phần) khi đó dao động tổng hợp có biên độ không đổi nhưng lệch pha so với dao động thứ nhất một góc ${\alpha _2}$ , với ${\alpha _1} + {\alpha _2} = \frac{\pi }{2}$ . Giá trị ban đầu của biên độ A2 là
Câu 28: Chuyển động của một vật là tổng hợp của hai dao động điều hòa cùng phương cùng tần số có các phương trình là x1 = 4cos(10t + π/4) cm; x2 = 3cos(10t + 3π/4) cm. Gia tốc cực đại của vật trong quá trình dao động là
Câu 29: Trên một sợi dây AB dài 90 cm, hai đầu cố định, đang có sóng dừng với tần số 50 Hz. Biết tốc độ truyền sóng trên dây là 10 m/s. Số bụng sóng trên dây là
Câu 30: M, N và P là 3 vị trí cân bằng liên tiếp trên một sợi dây đang có sóng dừng mà các phần tử tại đó dao động với cùng biên độ bằng $\sqrt 3 $ cm. Biết vận tốc tức thời của hai phần tử tại N và P thỏa mãn ${v_N}.{v_P} \ge 0$ ; MN = 40 cm, NP = 20 cm; tần số góc của sóng là 20 rad/s. Tốc độ dao động của phần tử tại trung điểm của NP khi sợi dây có dạng một đoạn thẳng bằng
Câu 31: Có thể tạo sóng dừng trên một sợi dây đàn hồi với hai tần số liên tiếp là 30 Hz và 50 Hz. Khi sóng truyền trên dây với tần số 50 Hz thì kể cả hai đầu dây, số bụng sóng trên dây là
Câu 32: Đặt điện áp xoay chiều áp $u = {U_0}\cos \omega t\,\,\left( V \right)$ vào mạch điện gồm cuộn dây có điện trở và độ tự cảm L, nối tiếp với tụ C thay đổi được. Khi C = C1 thì công suất của mạch là P1 = 200W và cường độ dòng điện qua mạch là i = I0cos(ωt + π/3) (A). Khi C = C2 thì hiệu điện thế hai đầu mạch cùng pha với dòng điện và công suất mạch là P2. Giá trị của P2 là
Câu 33: Đặt điện áp $u = {U_0}cos(100\pi t + \frac{\pi }{6})\,\,\,\left( V \right)$ vào hai đầu đoạn mạch mắc nối tiếp gồm điện trở thuần, cuộn cảm thuần và tụ điện thì cường độ dòng điện qua mạch là $i = {U_0}cos\left( {100\pi t + \frac{\pi }{6}} \right)\,\,\,\left( A \right)$ . Hệ số công suất của đoạn mạch bằng
Câu 34: Cho đoạn mạch AB gồm hai đoạn mạch AM nối tiếp với MB. Biết đoạn MA gồm R nối tiếp với C và MB có cuộn cảm có độ tự cảm L và điện trở r. Đặt vào AB một điện áp xoay chiều $u = U\sqrt 2 \cos \omega t\left( V \right)$ . Biết $R = r = \sqrt {\frac{L}{C}}$, điện áp hiệu dụng giữa hai đầu MB lớn gấp $n = \sqrt 3$ điện áp hai đầu AM. Hệ số công suất của đoạn mạch có giá trị là:
Câu 35: Một nguồn âm là nguồn điểm O phát âm công suất không đổi, truyền đẳng hướng. Coi môi trường không hấp thụ âm. Một máy đo mức cường độ âm di chuyển từ A đến B trên đoạn thẳng AB (với OA = 3 m) với tốc độ không đổi bằng 1,2 m/s. Máy đo được mức cường độ âm tại A và B đều bằng L1, tại C mức cường độ âm cực đại là Lmax. Biết Lmax – L1 = 3 dB. Thời gian máy di chuyển từ A đến B gần nhất với giá trị nào sau đây?
Câu 36: Một nguồn âm O có công suất P0 = 0,6 W phát sóng âm dạng hình cầu. Cường độ âm tại điểm A cách nguồn 3 m là
Câu 37: Một nguồn âm đặt tại O trong môi trường đẳng hướng. Hai điểm M và N trong môi trường đó tạo với O thành một tam giác vuông cân tại O. Mức cường độ âm tại M và tại N bằng nhau và bằng 23dB. Mức cường độ âm lớn nhất mà một máy đo thu được tại một điểm trên đoạn MN là
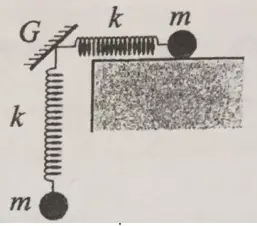
Câu 38: Hai con lắc lò xo giống hệt nhau được gắn vào điểm G của một giá cố định như hình bên. Trên phương nằm ngang và phương thẳng đứng, các con lắc đang dao động điều hòa với cùng biên độ 12 cm, cùng chu kì T nhưng vuông pha với nhau. Gọi FG là độ lớn hợp lực của các lực do hai lò xo tác dụng lên giá. Biết khoảng thời gian ngắn nhất giữa hai lần mà FG bằng trọng lượng của vật nhỏ của con lắc là $\frac{T}{4}$. Lấy g = 10 m/s2. Giá trị của T gần nhất với giá trị nào sau đây?
Câu 39: Trong thí nghiệm giao thoa sóng ở mặt nước, hai nguồn kết hợp đặt tại hai điểm A và B, dao động cùng pha theo phương thẳng đứng, phát ra hai sóng lan truyền trên mặt nước với bước sóng l. Ở mặt nước, C và D là hai điểm sao cho ABCD là hình vuông. Trên cạnh BC có 6 điểm cực đại giao thoa và 7 điểm cực tiểu giao thoa, trong đó P là điểm cực đại giao thoa gần B nhất và Q là điểm cực đại giao thoa gần C nhất. Khoảng cách xa nhất có thể giữa hai điểm P và Q là
Câu 40: Trong thí nghiệm Y-âng về giao thoa ánh sáng, hai khe hẹp cách nhau 0,6 mm và cách màn quan sát 1,2 m. Chiếu sáng các khe bằng ánh sáng đơn sắc có bước sóng l (380 nm l 760 nm). Trên màn, điểm M cách vân trung tâm 2,3 mm là vị trí của một vân tối. Giá trị của l gần nhất với giá trị nào sau đây?