Thi thử tốt nghiệp THPT quốc gia môn Vật Lý online – Đề thi của trường THPT Phú Xuân 2022 giúp bạn đánh giá chính xác mức độ hiểu bài thông qua nội dung bám sát chương trình học. Các câu hỏi được thiết kế khoa học giúp bạn học mà không cảm thấy áp lực. Đặc biệt phù hợp với học sinh muốn cải thiện điểm số. Thông qua quá trình làm bài, bạn có thể xác định phần kiến thức còn yếu. Điều này giúp việc học trở nên có mục tiêu rõ ràng hơn.
Thi thử tốt nghiệp THPT quốc gia môn Vật Lý online – Đề thi của trường THPT Phú Xuân 2022
Câu 1: Khi một nhạc cụ phát ra một âm cơ bản có tần số ${{f}_{0}}$ thì nhạc cụ đó đồng thời phát ra một loạt các họa âm có tần số $2{{f}_{0}}$, $3{{f}_{0}}$,$4{{f}_{0}}$ ... Họa âm thứ tư có tần số là
Câu 2: Trong hệ SI, đơn vị của hiệu điện thế là
Câu 3: Trong thí nghiệm Young về giao thoa ánh sáng, hai khe hẹp cách nhau một khoảng $a$ và cách màn quan sát một khoảng $D$. Chiếu sáng các khe bằng ánh sáng đơn sắc có bước sóng $\lambda $. Trên màn, khoảng cách từ vị trí có vân tối đến vân trung tâm là
Câu 4: Đặt điện áp xoay chiều vào hai đầu đoạn mạch có $RLC$mắc nối tiếp thì cảm kháng và dung kháng của đoạn mạch lần lượt là ${{Z}_{L}}$ và ${{Z}_{C}}$. Điện áp giữa hai đầu đoạn mạch trễ pha hơn cường độ dòng điện trong mạch khi
Câu 5: : Một con lắc đơn có vật nhỏ khối lượng $m$ đang dao động điều hòa ở nơi có gia tốc trọng trường $g$. Khi vật qua vị trí có li độ góc $\alpha $ thì phương trình động lực học cho vật có dạng ${\alpha }''+\frac{g}{l}\alpha =0$ Đại lượng $\frac{g}{l}$ có đơn vị là
Câu 6: Hai dao động điều hòa cùng phương, cùng tần số có pha ban đầu là ${{\varphi }_{1}}$ và ${{\varphi }_{2}}$. Hai dao động ngược pha khi hiệu ${{\varphi }_{2}}-{{\varphi }_{1}}$ có giá trị bằng
Câu 7: Trong y học, tia nào sau đây thường được sử dụng để chiếu điện, chụp điện?
Câu 8: Trong sóng cơ cho tốc độ lan truyền dao động trong môi trường là $v$, chu kì của sóng là $T$. Bước sóng của sóng này bằng
Câu 9: Số nuclon có trong hạt nhân ${}_{3}^{6}Li$ là
Câu 10: Trong điện xoay chiều, các đại lượng nào sau đây không có giá trị hiệu dụng?
Câu 11: Sau các cơn mưa chúng ta thường quan sát thấy cầu vồng. Sự hình thành cầu vồng được giải thích chủ yếu dựa vào hiện tượng
Câu 12: Một máy biến áp lí tưởng có số vòng dây của cuộn sơ cấp lớn hơn số vòng dây của cuộn thứ cấp. Khi hoạt động ở chế độ có tải, máy biến áp này có tác dụng làm
Câu 13: Tia lửa điện có bản chất là dòng điện
Câu 14: Dao động của một vật là dao động cưỡng bức dưới tác dụng của ngoại lực $f={{F}_{0}}\cos \left( 20\pi t \right)$, ${{F}_{0}}$ không đổi. Chu kì dao động của vật là
Câu 15: Bộ phận nào sau đây không có trong sơ đồ khối của một máy quang phổ lăng kính?
Câu 16: Một con lắc lò xo gồm vật nhỏ khối lượng $m$ và lò xo nhẹ có độ cứng $k$ đang dao động điều hòa. Khi vật qua vị trí có li độ $x$ thì gia tốc của vật là $a$. Thương số $\frac{a}{x}$ bằng
Câu 17: Khi nói về thuyết lượng tử ánh sáng, phát biểu nào sau đây sai?
Câu 18: Gọi ${{m}_{p}}$ là khối lượng của proton, ${{m}_{n}}$ là khối lượng của nơtron, ${{m}_{X}}$ là khối lượng của hạt nhân ${}_{Z}^{A}X$và $c$ là tốc độ của ánh sáng trong chân không. Đại lượng $\left( Z{{m}_{p}}+\left( A-Z \right){{m}_{n}}-{{m}_{X}} \right)\frac{{{c}^{2}}}{A}$ được gọi là
Câu 19: Trong thí nghiệm giao thoa sóng ở mặt nước, hai nguồn kết hợp dao động cùng pha theo phương thẳng đứng. Biết sóng truyền trên mặt nước với bước sóng $\lambda $. Ở mặt nước, $M$ là điểm cực đại giao thoa cách hai nguồn những khoảng là ${{d}_{1}}$ và ${{d}_{2}}$. Công thức nào sau đây đúng?
Câu 20: Khi nói về ánh sáng đơn sắc, phát biểu nào sau đây sai?
Câu 21: Đặt điện áp xoay chiều vào hai đầu đoạn mạch gồm điện trở $R$ mắc nối tiếp với cuộn cảm thuần thì cảm kháng và tổng trở của đoạn mạch lần lượt là ${{Z}_{L}}$ và $Z$. Công thức nào sau đây đúng độ lệch pha giữa điện áp hai đầu mạch và cường độ dòng điện trong mạch?
Câu 22: Trong điện trường đều, hai điểm $M$ và $N$ cùng nằm trên một đường sức điện và đường sức điện có chiều từ $M$ đến $N$. Theo chiều từ $M$ đến $N$ thì điện thế
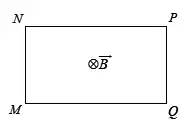
Câu 23: Một khung dây dẫn kín hình chữ nhật $MNPQ$ đặt cố định trong từ trường đều. Hướng của từ trường $\overrightarrow{{{B}_{{}}}}$ vuông góc với mặt phẳng khung dây như hình bên. Trong khung dây có dòng điện chạy theo chiều $NMQPN$. Lực từ tác dụng lên cạnh $MN$ cùng hướng với
Câu 24: Một con lắc lò xo gồm vật nhỏ và lò xo nhẹ có độ cứng 50 N/m. Khi con lắc dao động điều hòa với biên độ 5 cm thì động năng cực đại của con lắc là
Câu 25: Trong thí nghiệm Young về giao thoa ánh sáng, nguồn sáng phát ra ánh sáng đơn sắc có bước sóng 500 nm. Hai khe hẹp cách nhau một khoảng $a$ và cách màn quan sát một khoảng $D$ với $D=1200a$. Trên màn, khoảng vân giao thoa là
Câu 26: Cho phản ứng nhiệt hạch ${}_{1}^{1}H+{}_{1}^{3}H$→ ${}_{2}^{4}He$. Biết khối lượng của ${}_{1}^{1}H$;${}_{1}^{3}H$ và${}_{2}^{4}He$ lần lượt là 1,0073 u; 3,0155 u và 4,0015 u. Lấy $1u=931,5$$\tfrac{MeV}{{{c}^{2}}}$. Năng lượng tỏa ra của phản ứng này là
Câu 27: Đặt điện áp xoay chiều vào hai đầu đoạn mạch gồm điện trở 20 Ω mắc nối tiếp với cuộn cảm thuần thì cảm kháng của đoạn mạch là 30 Ω. Hệ số công suất của đoạn mạch này bằng
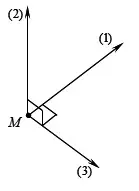
Câu 28: Sóng điện từ lan truyền qua một điểm $M$ trong không gian. Các vecto (1), (2) và (3) biểu diễn các vecto $\overrightarrow{{{v}_{{}}}}$, $\overrightarrow{{{E}_{{}}}}$ và $\overrightarrow{{{B}_{{}}}}$. Kết luận nào sau đây là đúng?
Câu 29: Trong chân không, một tia $X$ và một tia tử ngoại có bước sóng lần lượt là 0,2 nm và 300 nm. Tỉ số giữa năng lượng mỗi photon của tia $X$ và năng lượng mỗi photon của tia tử ngoại là
Câu 30: Biết cường độ âm chuẩn là ${{10}^{-12}}$$\tfrac{W}{{{m}^{2}}}$. Tại một điểm có cường độ âm là ${{10}^{-6}}$$\tfrac{W}{{{m}^{2}}}$ thì mức cường độ âm tại đó là
Câu 31: Trong thí nghiệm Young về giao thoa ánh sáng, khoảng cách giữa hai khe hẹp là $a$ và cách màn quan sát một khoảng $D$. Chiếu sáng các khe bằng ánh sáng đơn sắc có bước sóng $\lambda $. Trên màn, $M$ và $N$ là hai vị trí của 2 vân sáng. Biết $MN=7,7$mm và khoảng cách giữa 2 vân tối xa nhau nhất trong khoảng $MN$ là 6,6 mm. Giữ nguyên các điều kiện ban đầu, thay ánh áng có bước sóng $\lambda $ bằng ánh sáng có bước sóng ${\lambda }'=\frac{4}{5}\lambda $. Vị trí cho vân sáng bậc 5 của bức xạ ${\lambda }'$ cách vân trung tâm
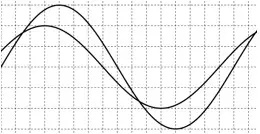
Câu 32: Đặt điện áp xoay chiều vào hai đầu đoạn mạch có $RLC$ mắc nối tiếp. Để xác định hệ số công suất của đoạn mạch này, một học sinh dùng dao động kí điện tử để hiển thị đồng thời đồ thị điện áp tức thời giữa hai đầu đoạn mạch và điện áp tức thời giữa hai đầu điện trở $R$ và cho kết quả như hình bên (các đường hình sin). Hệ số công suất của đoạn mạch này là
Câu 33: Đặt điện áp xoay chiều $u=U\sqrt{2}\cos \left( \omega t \right)$ vào hai đầu đoạn mạch có $RLC$mắc nối tiếp, trong đó tụ điện có điện dung $C$ thay đổi được. Thay đổi $C$ để điện áp hiệu dụng giữa hai đầu tụ điện đạt giá trị cực đại, giá trị cực đại này là 200 V. Khi đó, điện áp hiệu dụng giữa hai đầu điện trở $R$ có thể nhận giá trị lớn nhất là
Câu 34: Một sợi dây đàn hồi $AB$ căng ngang có đầu $B$ cố định, đầu $A$ nối với một máy rung. Khi máy rung hoạt động, đầu $A$ dao động điều hòa thì trên dây có sóng dừng với 4 bụng sóng. Đầu $A$ được coi là một nút sóng. Tăng tần số của máy rung thêm một lượng 12 Hz thì trên dây có sóng dừng với 6 bụng sóng. Biết tốc độ truyền sóng trên dây không đổi. Tần số nhỏ nhất của máy rung để trên dây có sóng dừng là
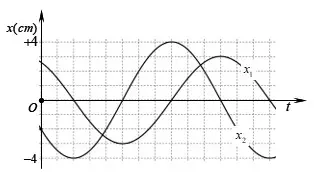
Câu 35: Dao động của một vật có khối lượng 100 g là tổng hợp của hai dao động điều hòa cùng phương có li độ ${{x}_{1}}$ và ${{x}_{2}}$. Hình bên là đồ thị biểu diễn sự phụ thuộc của ${{x}_{1}}$ và ${{x}_{2}}$ theo thời gian $t$. Theo phương pháp giản đồ Frenel, dao động của vật được biểu diễn bằng một vecto quay. Biết tốc độ góc của vecto quay này là $\frac{5\pi }{3}$$\tfrac{rad}{s}$. Động năng của vật tại thời điểm $t=0,2$s là
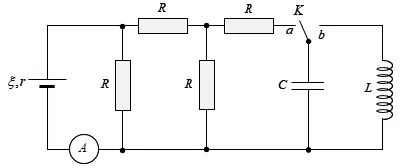
Câu 36: Dùng mạch điện như hình bên để tạo dao động điện từ, trong đó $\xi =5$V, $r=1$Ω và các điện trở $R$ giống nhau. Bỏ qua điện trở của ampe kế. Ban đầu khóa $K$ đóng ở chốt $a$, chỉ số ampe kế là 1 A. Chuyển $K$ đóng vào chốt $b$, trong mạch $LC$ có dao động điện từ. Biết rằng, khoảng thời gian ngắn nhất để từ thông riêng của cuộn cảm giảm từ giá trị cực đại ${{\Phi }_{0}}$ xuống 0 là $\tau $. Giá trị của biểu thức $\frac{\pi {{\Phi }_{0}}}{\tau }$ bằng
Câu 37: Để xác định thể tích máu trong cơ thể, người ta tiêm vào trong máu một người 10 ml một dung dịch chứa chất phóng xạ ${}^{24}Na$ với nồng độ ${{10}^{-3}}$$\tfrac{mol}{l\acute{i}t}$. Cho biết chu kì bán rã của ${}^{24}Na$ là 15 giờ. Sau 6 giờ kể từ thời điểm tiêm vào cơ thể người ta lấy ra 10 ml máu và tìm thấy có $1,{{78.10}^{-8}}$ mol chất phóng xạ ${}^{24}Na$. Giả thiết với thời gian trên thì chất phóng xạ phân bố đều trong cơ thể. Thể tích máu của người đó là
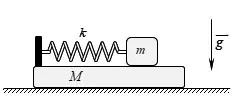
Câu 38: Con lắc lò xo gồm vật nhỏ có khối lượng $m=100$g, lò xo có độ cứng $k=50$N.m một đầu gắn vào vật nhỏ đầu còn lại gắn vào vật $M=100$g đang nằm trên một bề mặt nằm ngang. Bỏ qua mọi ma sát, cho rằng $M$ đủ dài để $m$ luôn di chuyển trên nó, lấy ${{\pi }^{2}}=10$. Ban đầu cố định $M$, kéo $m$ lệch khỏi vị trí cân bằng của nó một đoạn nhỏ. Thả tự do cho hệ, khi đó chu kì dao động của $m$ bằng
Câu 39: Trong thí nghiệm giao thoa sóng ở mặt nước, hai nguồn kết hợp đặt tại hai điểm $A$ và $B$, dao động cùng pha theo phương thẳng đứng. Trên đoạn $AB$ quan sát được 13 cực đại giao thoa. Ở mặt nước, đường tròn $(C)$ có tâm $O$ thuộc trung trực $AB$ và bán kính $a$ không đổi ($2a<AB$). Khi di chuyển $(C)$ trên mặt nước sao cho tâm $O$ luôn nằm trên đường trung trực của $AB$ thì thấy trên $(C)$ có tối đa 12 cực đại giao thoa. Khi trên $(C)$ có 12 điểm cực đại giao thoa thì trong số đó có 4 điểm mà phần tử tại đó dao động ngược pha với nguồn. Đoạn thẳng $AB$ gần nhất giá trị nào sau đây?
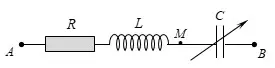
Câu 40: Cho đoạn mạch điện xoay chiều như hình vẽ. $R$ là điện trở thuần, $L$ là cuộn cảm thuần, tụ điện $C$ có điện dung thay đổi được. Đặt vào hai đầu đoạn mạch một điện áp xoay chiều có giá trị hiệu dụng không đổi ${{U}_{AB}}=12$V. Khi $C={{C}_{1}}$ thì ${{U}_{AM}}=16$ V, ${{U}_{MB}}=20$V. Khi $C={{C}_{2}}$ thì ${{U}_{AM}}=10$ V. Giá trị ${{U}_{MB}}$ lúc này bằng