Đề thi thử THPT QG năm 2021 môn Vật Lý online – Đề thi của Trường THPT Võ Văn Kiệt giúp bạn luyện tập thường xuyên để ghi nhớ lâu hơn thông qua các câu hỏi được chọn lọc kỹ lưỡng. Các câu hỏi được phân bổ hợp lý theo mức độ nhận thức giúp bạn không bị quá tải. Đặc biệt phù hợp với người chuẩn bị cho các kỳ kiểm tra quan trọng. Thông qua quá trình làm bài, bạn có thể biết được nội dung nào cần ôn lại. Điều này giúp việc học trở nên hiệu quả hơn.
Đề thi thử THPT QG năm 2021 môn Vật Lý online – Đề thi của Trường THPT Võ Văn Kiệt
Câu 1: Quạt cây sử dụng trong nhà có cánh quạt được gắn với trục quay và trục này được gắn với:
Câu 2: Sóng điện từ lan truyền trong không gian, tại một điểm dao động của điện trường và từ trường luôn:
Câu 3: Một kim loại có công thoát electron là A. Biết hằng số Plăng là h và tốc độ ánh sáng truyền trong chân không là c. Giới hạn quang điện của kim loại là:
Câu 4: Chọn phát biểu đúng. Tia hồng ngoại:
Câu 5: Trong phương trình dao động điều hòa: $x=A\cos \left( \omega t+\varphi \right)$, radian trên giây $\left( rad/s \right)$ là đơn vị đo của đại lượng:
Câu 6: Hạt nhân $_{Z}^{A}X$ có số prôtôn là:
Câu 7: Tính cường độ điện trường do một điện tích điểm $Q=+{{4.10}^{-9}}C$ gây ra tại một điểm cách nó 5 cm trong chân không.
Câu 8: Hiện tượng hai sóng trên mặt nước gặp nhau tạo nên các gợn sóng ổn định gọi là hiện tượng:
Câu 9: Một vật dao động điều hòa theo phương trình $x=A\cos \left( \omega t+\varphi \right)\left( A>0,\omega >0 \right)$. Pha của dao động ở thời điểm t là:
Câu 10: Trong máy phát điện xoay chiều một pha, phần cảm có p cặp cực, quay với tốc độ n vòng/phút. Dòng điện do máy phát ra có tần số là:
Câu 11: Chiếu chùm ánh sáng gồm 5 ánh sáng đơn sắc khác nhau là đỏ, cam, vàng, lục và tím đi từ nước ra không khí, thấy ánh sáng màu vàng ló ra ngoài song song với mặt nước. Xác định số bức xạ mà ta có thể quan sát được phía trên mặt nước?
Câu 12: Mạch dao động gồm một tụ điện có điện dung $10\mu F$ và một cuộn dây thuần cảm có độ tự cảm $L=2mH$. Khi hiệu điện thế ở hai đầu tụ điện là 4 V thì cường độ dòng điện trong mạch bằng 0,02 A. Hiệu điện thế cực đại giữa hai bản tụ là:
Câu 13: Trong một thí nghiệm Y-âng về giao thoa ánh sáng, khoảng cách giữa hai khe là $a=0,5\ mm$, khoảng cách từ mặt phẳng chứa hai khe đến màn quan sát là $D=2m$. Nguồn ánh sáng phát ra ánh sáng đơn sắc có bước sóng $0,5\mu m$. Trên màn khoảng cách giữa một vân sáng và một vân tối cạnh nhau bằng:
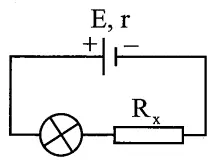
Câu 14: Cho mạch điện như hình vẽ. Biết $E=12\ V,r=4\Omega $, bóng đèn thuộc loại $6\,V-\ 6\ W$. Để đèn sáng bình thường thì giá trị của là:
Câu 15: Hạt nhân nào sau đây có thể phân hạch:
Câu 16: Độ to là một đặc tính sinh lí của âm phụ thuộc vào:
Câu 17: Khi nói về tính chất của tia tử ngoại, phát biểu nào sau đây là sai?
Câu 18: Một con lắc đơn có chiều dài 160 cm, dao động điều hòa với biên độ dài 16 cm. Biên độ góc của dao động là:
Câu 19: Cho một đoạn mạch RC có $R=50\Omega ,C=\frac{{{2.10}^{-4}}}{\pi }F$. Đặt vào hai đầu đoạn mạch một điện áp $u={{U}_{0}}\cos \left( 100\pi t-\frac{\pi }{4} \right)V$. Tổng trở của mạch bằng:
Câu 20: Hai sóng chạy có vận tốc 750 m/s, truyền ngược chiều nhau và giao thoa nhau tạo thành sóng dừng. Khoảng cách từ nút thứ 1 đến nút thứ 5 bằng 6 m. Tần số các sóng chạy bằng:
Câu 21: Đặt điện áp xoay chiều vào hai đầu đoạn mạch có R, L, C mắc nối tiếp. Biết ${{R}_{0}}=30\Omega $, cuộn cảm thuần có cảm kháng $20\Omega $ và tụ điện có dung kháng $60\Omega $. Hệ số công suất của mạch là:
Câu 22: Xét nguyên tử hiđrô theo mẫu nguyên tử Bo. Biết bán kính Bo là ${{r}_{0}}$. Êlectron không có bán kính quỹ đạo dừng nào sau đây?
Câu 23: Một vật dao động điều hòa theo phương trình $x=10\cos \left( 10\pi t+\frac{\pi }{3} \right)cm$. Thời gian ngắn nhất kể từ lúc vật bắt đầu dao động đến lúc vật có tốc độ $50\pi \ cm/s$ là:
Câu 24: Một chất điểm dao động điều hòa theo phương trình $x=2\cos 2\pi t\ cm$; tại thời điểm $t=\frac{1}{3}s$ chất điểm có vận tốc bằng:
Câu 25: Đặt điện áp xoay chiều có giá trị cực đại là 200 V vào hai đầu một tụ điện thì cường độ dòng điện trong mạch có biểu thức $i=2\cos \left( 100\pi t+\frac{\pi }{3} \right)A$. Khi cường độ dòng điện $i=1\ A$ thì điện áp giữa hai đầu tụ điện có độ lớn bằng:
Câu 26: Dao động được ứng dụng trong thiết bị giảm xóc của ô tô là:
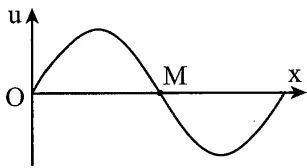
Câu 27: Trên một sợi dây dài đang có sóng ngang hình sin truyền qua theo chiều dương của trục Ox. Tại thời điểm t, một đoạn của sợi dây có hình dạng như hình bên. Hai phần tử trên dây là O và M dao động lệch pha nhau:
Câu 28: Vật sáng AB đặt trước một thấu kính hội tụ cho ảnh rõ nét trên màn cách vật 90 cm. Biết ảnh cao gấp hai lần vật. Tiêu cự của thấu kính là:
Câu 29: Thực hiện thí nghiệm Y-âng giao thoa ánh sáng, hai khe hẹp cách nhau 1 mm, nguồn sáng có bước sóng trong khoảng $0,38\mu m$ đến $0,76\mu m$ thì bề rộng quang phổ bậc 1 đo được trên màn là 0,38 mm. Dịch màn rời xa mặt phẳng chứa hai khe thêm một đoạn x thì bề rộng quang phổ bậc 1 trên màn đo được là 0,551 mm. Độ dịch chuyển của màn là:
Câu 30: Dao động của một chất điểm là tổng hợp của hai dao động điều hòa cùng phương, có phương trình ${{x}_{1}}=3\cos \left( \frac{2\pi }{3}t-\frac{\pi }{2} \right)cm;{{x}_{2}}=3\sqrt{3}\cos \left( \frac{2\pi }{3}t \right)cm$. Tại thời điểm hai dao động thành phần có cùng li độ thì li độ ${{x}_{1}}={{x}_{2}}$ của dao động tổng hợp của chất điểm là:
Câu 31: Một đám nguyên tử hiđrô đang ở trạng thái kích thích mà êlectron chuyển động trên quỹ đạo dừng N. Khi các êlectron chuyển về các quỹ đạo dừng bên trong thì quang phổ vạch phát xạ của đám nguyên tử đó có bao nhiêu vạch?
Câu 32: Một cuộn dây tròn có 100 vòng dây, mỗi vòng dây có bán kính $R=2,5\ cm$ và có cường độ dòng điện $I=\frac{1}{\pi }A$ chạy qua. Cảm ứng từ tại tâm cuộn dây có độ lớn bằng:
Câu 33: Một vật thực hiện đồng thời hai dao động điều hòa cùng phương cùng tần số có phương trình: ${{x}_{1}}=2\cos \left( 2\pi t-\frac{\pi }{3} \right)cm;{{x}_{2}}=2\cos \left( 2\pi t \right)cm$. Tốc độ trung bình của vật từ lúc bắt đầu chuyển động đến khi vật qua vị trí có động năng bằng thế năng lần thứ nhất là:
Câu 34: Đặt điện áp $u={{U}_{0}}\cos \left( 100\pi t+\frac{\pi }{3} \right)V$ vào hai đầu một cuộn cảm thuần có độ tự cảm $L=\frac{1}{\pi }H$. Ở thời điểm điện áp giữa hai đầu cuộn cảm là $100\sqrt{2}\ V$ thì cường độ dòng điện qua cuộn cảm là 2 A. Biểu thức của cường độ dòng điện qua cuộn cảm này là:
Câu 35: Kim loại có công thoát êlectron là 2,62 eV. Khi chiếu vào kim loại này hai bức xạ có bước sóng ${{\lambda }_{1}}=0,4\mu m$ và ${{\lambda }_{2}}=0,2\mu m$ thì hiện tượng quang điện:
Câu 36: Trong thí nghiệm Y-âng về giao thoa ánh sáng, hai khe ${{S}_{1}},{{S}_{2}}$ được chiếu bằng ánh sáng đơn sắc có bước sóng $\lambda $ thì tại vị trí điểm M trên màn quan sát với ${{S}_{2}}M-{{S}_{1}}M=3\mu m$ thu được vân sáng. Nếu thay ánh sáng đơn sắc bằng ánh sáng trắng có bước sóng từ $0,38\mu m$ đến $0,76\mu m$ và các điều kiện khác giữ nguyên thì tại M số bức xạ cho vân sáng là:
Câu 37: Một sợi dây đàn hồi dài 60 cm có một đầu cố định, đầu kia được gắn với một thiết bị rung có tần số f, trên dây tạo thành một sóng dừng ổn định với 4 bụng sóng, coi như hai đầu dây là hai nút sóng. Thời gian giữa 3 lần liên tiếp sợi dây duỗi thẳng là 0,02 s. Tốc độ truyền sóng trên dây là:
Câu 38: Đoạn mạch AB gồm điện trở $R=50\ \Omega $, cuộn dây có độ tự cảm $L=\frac{0,4}{\pi }H$ và điện trở $r=60\ \Omega $, tụ điện có điện dung C thay đổi được và mắc theo đúng thứ tự trên. Đặt vào hai đầu mạch một điện áp xoay chiều có dạng ${{u}_{AB}}=220\sqrt{2}\cos 100\pi t$ V, t tính bằng giây. Người ta thấy rằng khi $C={{C}_{m}}$ thì điện áp hiệu dụng ở hai đầu đoạn mạch chứa cuộn dây và tụ điện đạt cực tiểu ${{U}_{\min }}$. Giá trị của ${{C}_{m}}$ và ${{U}_{\min }}$ lần lượt là:
Câu 39: Dao động điện từ trong mạch dao động LC lí tưởng (gồm cuộn dây thuần cảm là một ống dây, tụ điện là tụ phẳng) là dao động điều hòa, khi từ trường đều trong lòng cuộn cảm bằng ${{B}_{1}}={{2.10}^{-4}}T$ thì cường độ điện trường đều trong tụ bằng ${{E}_{1}}=3\sqrt{11}{{.10}^{3}}\ V/m$. Khi từ trường đều trong lòng cuộn cảm bằng ${{B}_{2}}=\sqrt{2}{{.10}^{-3}}T$ thì cường độ điện trường đều trong tụ bằng ${{E}_{2}}=5\sqrt{2}{{.10}^{3}}\ V/m$. Giá trị cực đại của từ trường đều trong lòng cuộn và cường độ điện trường đều trong tụ lần lượt là:
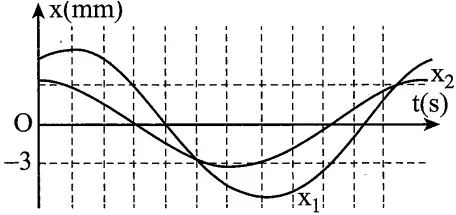
Câu 40: Hai chất điểm M, N dao động điều hòa trên các quỹ đạo song song, gần nhau dọc theo trục Ox, có li độ lần lượt là ${{x}_{1}}$ và ${{x}_{2}}$. Hình bên là đồ thị biểu diễn sự phụ thuộc của ${{x}_{1}}$ và ${{x}_{2}}$ theo thời gian t. Trong quá trình dao động, khoảng cách lớn nhất giữa hai chất điểm xét theo phương Ox là: